5  Static communication

Prerequisites

Key concepts and skills

Software and packages

library(carData)
library(datasauRus)
library(ggmap)
library(janitor)
library(knitr)
library(maps)
library(mapproj)
library(modelsummary)
library(opendatatoronto)
library(patchwork)
library(tidygeocoder)
library(tidyverse)
library(troopdata)
library(WDI)

5.1 Introduction

When telling stories with data, we would like the data to do much of the work of convincing our reader. The paper is the medium, and the data are the message. To that end, we want to show our reader the data that allowed us to come to our understanding of the story. We use graphs, tables, and maps to help achieve this.

Try to show the observations that underpin our analysis. For instance, if your dataset consists of 2,500 responses to a survey, then at some point in the paper you should have a plot/s that contains each of the 2,500 observations, for every variable of interest. To do this we build graphs using ggplot2 which is part of the core tidyverse and so does not have to be installed or loaded separately. In this chapter we go through a variety of different options including bar charts, scatterplots, line plots, and histograms.

In contrast to the role of graphs, which is to show each observation, the role of tables is typically to show an extract of the dataset or to convey various summary statistics, or regression results. We will build tables primarily using knitr. Later we will use modelsummary to build tables related to regression output.

Finally, we cover maps as a variant of graphs that are used to show a particular type of data. We will build static maps using ggmap after having obtained geocoded data using tidygeocoder.

5.2 Graphs

A world turning to a saner and richer civilization will be a world turning to charts.

Karsten (1923, 684)

Graphs are a critical aspect of compelling data stories. They allow us to see both broad patterns and details (Cleveland [1985] 1994, 5). Graphs enable a familiarity with our data that is hard to get from any other method. Every variable of interest should be graphed.

The most important objective of a graph is to convey as much of the actual data, and its context, as possible. In a way, graphing is an information encoding process where we construct a deliberate representation to convey information to our audience. The audience must decode that representation. The success of our graph depends on how much information is lost in this process so the decoding is a critical aspect (Cleveland [1985] 1994, 221). This means that we must focus on creating effective graphs that are suitable for our specific audience.

To see why graphing the actual data is important, after installing and loading datasauRus consider the datasaurus_dozen dataset.

datasaurus_dozen
# A tibble: 1,846 × 3
   dataset     x     y
   <chr>   <dbl> <dbl>
 1 dino     55.4  97.2
 2 dino     51.5  96.0
 3 dino     46.2  94.5
 4 dino     42.8  91.4
 5 dino     40.8  88.3
 6 dino     38.7  84.9
 7 dino     35.6  79.9
 8 dino     33.1  77.6
 9 dino     29.0  74.5
10 dino     26.2  71.4
# ℹ 1,836 more rows

The dataset consists of values for “x” and “y”, which should be plotted on the x-axis and y-axis, respectively. There are 13 different values in the variable “dataset” including: “dino”, “star”, “away”, and “bullseye”. We focus on those four and generate summary statistics for each (Table 5.1).

# Based on: https://juliasilge.com/blog/datasaurus-multiclass/
datasaurus_dozen |>
  filter(dataset %in% c("dino", "star", "away", "bullseye")) |>
  summarise(across(c(x, y), list(mean = mean, sd = sd)),
            .by = dataset) |>
  kable(col.names = c("Dataset", "x mean", "x sd", "y mean", "y sd"),
        booktabs = TRUE, digits = 1)
Table 5.1: Mean and standard deviation for four datasauRus datasets
Dataset x mean x sd y mean y sd
dino 54.3 16.8 47.8 26.9
away 54.3 16.8 47.8 26.9
star 54.3 16.8 47.8 26.9
bullseye 54.3 16.8 47.8 26.9

Notice that the summary statistics are similar (Table 5.1). Despite this it turns out that the different datasets are actually very different beasts. This becomes clear when we plot the data (Figure 5.1).

datasaurus_dozen |>
  filter(dataset %in% c("dino", "star", "away", "bullseye")) |>
  ggplot(aes(x = x, y = y, colour = dataset)) +
  geom_point() +
  theme_minimal() +
  facet_wrap(vars(dataset), nrow = 2, ncol = 2) +
  labs(color = "Dataset")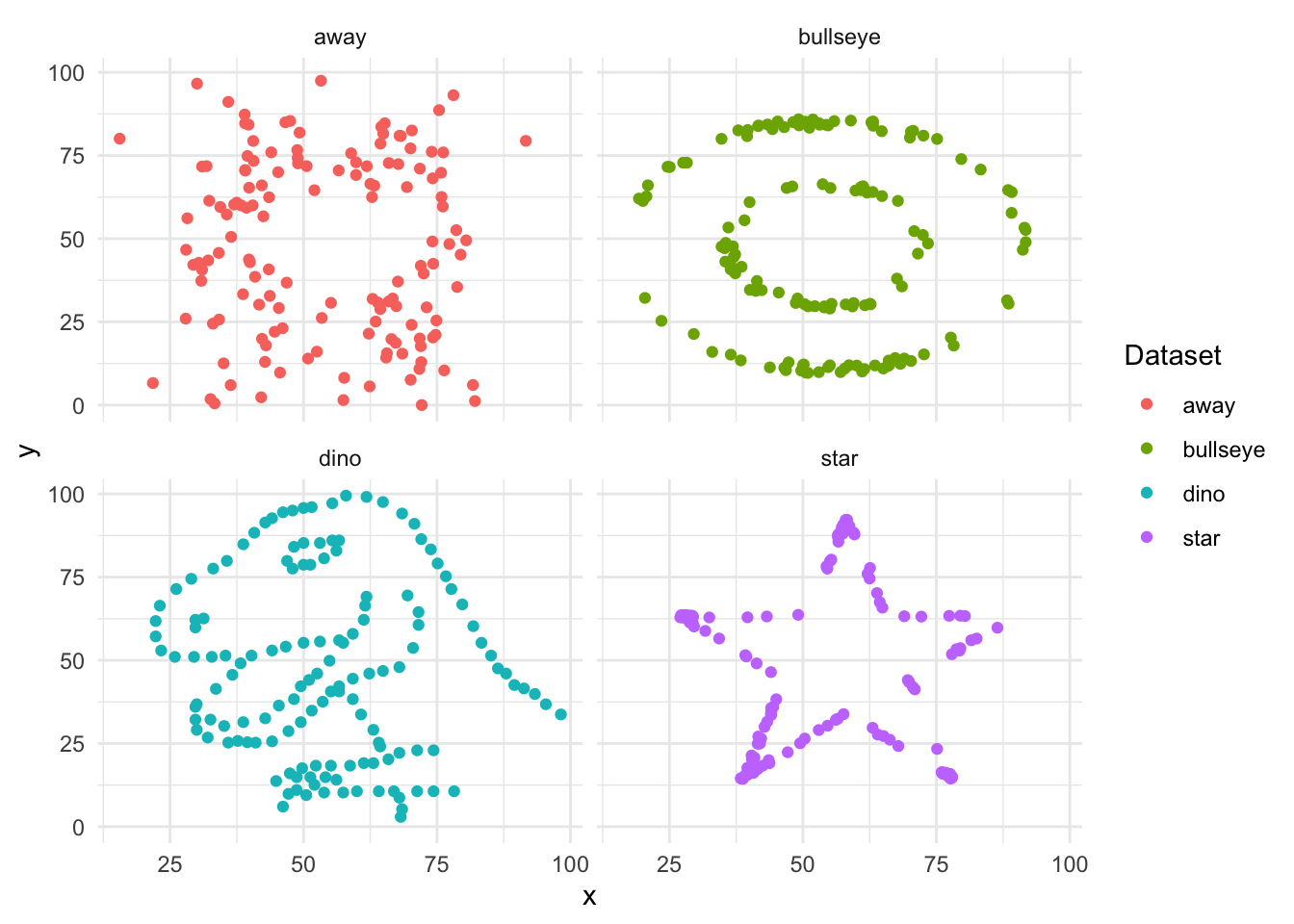

Figure 5.1: Graph of four datasauRus datasets

We get a similar lesson—always plot your data—from “Anscombe’s Quartet”, created by the twentieth century statistician Frank Anscombe. The key takeaway is that it is important to plot the actual data and not rely solely on summary statistics.

head(anscombe)
  x1 x2 x3 x4   y1   y2    y3   y4
1 10 10 10  8 8.04 9.14  7.46 6.58
2  8  8  8  8 6.95 8.14  6.77 5.76
3 13 13 13  8 7.58 8.74 12.74 7.71
4  9  9  9  8 8.81 8.77  7.11 8.84
5 11 11 11  8 8.33 9.26  7.81 8.47
6 14 14 14  8 9.96 8.10  8.84 7.04

Anscombe’s Quartet consists of eleven observations for four different datasets, with x and y values for each observation. We need to manipulate this dataset with pivot_longer() to get it into the “tidy” format discussed in Online Appendix A.

# From: https://www.njtierney.com/post/2020/06/01/tidy-anscombe/
# And the pivot_longer() vignette.

tidy_anscombe <-
  anscombe |>
  pivot_longer(
    everything(),
    names_to = c(".value", "set"),
    names_pattern = "(.)(.)"
  )

We can first create summary statistics (Table 5.2) and then plot the data (Figure 5.2). This again illustrates the importance of graphing the actual data, rather than relying on summary statistics.

tidy_anscombe |>
  summarise(
    across(c(x, y), list(mean = mean, sd = sd)),
    .by = set
    ) |>
  kable(
    col.names = c("Dataset", "x mean", "x sd", "y mean", "y sd"),
    digits = 1, booktabs = TRUE
  )
Table 5.2: Mean and standard deviation for Anscombe’s quartet
Dataset x mean x sd y mean y sd
1 9 3.3 7.5 2
2 9 3.3 7.5 2
3 9 3.3 7.5 2
4 9 3.3 7.5 2 
tidy_anscombe |>
  ggplot(aes(x = x, y = y, colour = set)) +
  geom_point() +
  geom_smooth(method = lm, se = FALSE) +
  theme_minimal() +
  facet_wrap(vars(set), nrow = 2, ncol = 2) +
  labs(colour = "Dataset") +
  theme(legend.position = "bottom")

Figure 5.2: Recreation of Anscombe’s Quartet

5.2.1 Bar charts

We typically use a bar chart when we have a categorical variable that we want to focus on. We saw an example of this in Chapter 2 when we constructed a graph of the number of occupied beds. The geometric object—a “geom”—that we primarily use is geom_bar(), but there are many variants to cater for specific situations. To illustrate the use of bar charts, we use a dataset from the 1997-2001 British Election Panel Study that was put together by Fox and Andersen (2006) and made available with BEPS, after installing and loading carData.

beps <- 
  BEPS |> 
  as_tibble() |> 
  clean_names() |> 
  select(age, vote, gender, political_knowledge)

The dataset consists of which party the respondent supports, along with various demographic, economic, and political variables. In particular, we have the age of the respondent. We begin by creating age-groups from the ages, and making a bar chart showing the frequency of each age-group using geom_bar() (Figure 5.3 (a)).

beps <-
  beps |>
  mutate(
    age_group =
      case_when(
        age < 35 ~ "<35",
        age < 50 ~ "35-49",
        age < 65 ~ "50-64",
        age < 80 ~ "65-79",
        age < 100 ~ "80-99"
      ),
    age_group = 
      factor(age_group, levels = c("<35", "35-49", "50-64", "65-79", "80-99"))
  )
beps |>
  ggplot(mapping = aes(x = age_group)) +
  geom_bar() +
  theme_minimal() +
  labs(x = "Age group", y = "Number of observations")

beps |> 
  count(age_group) |> 
  ggplot(mapping = aes(x = age_group, y = n)) +
  geom_col() +
  theme_minimal() +
  labs(x = "Age group", y = "Number of observations")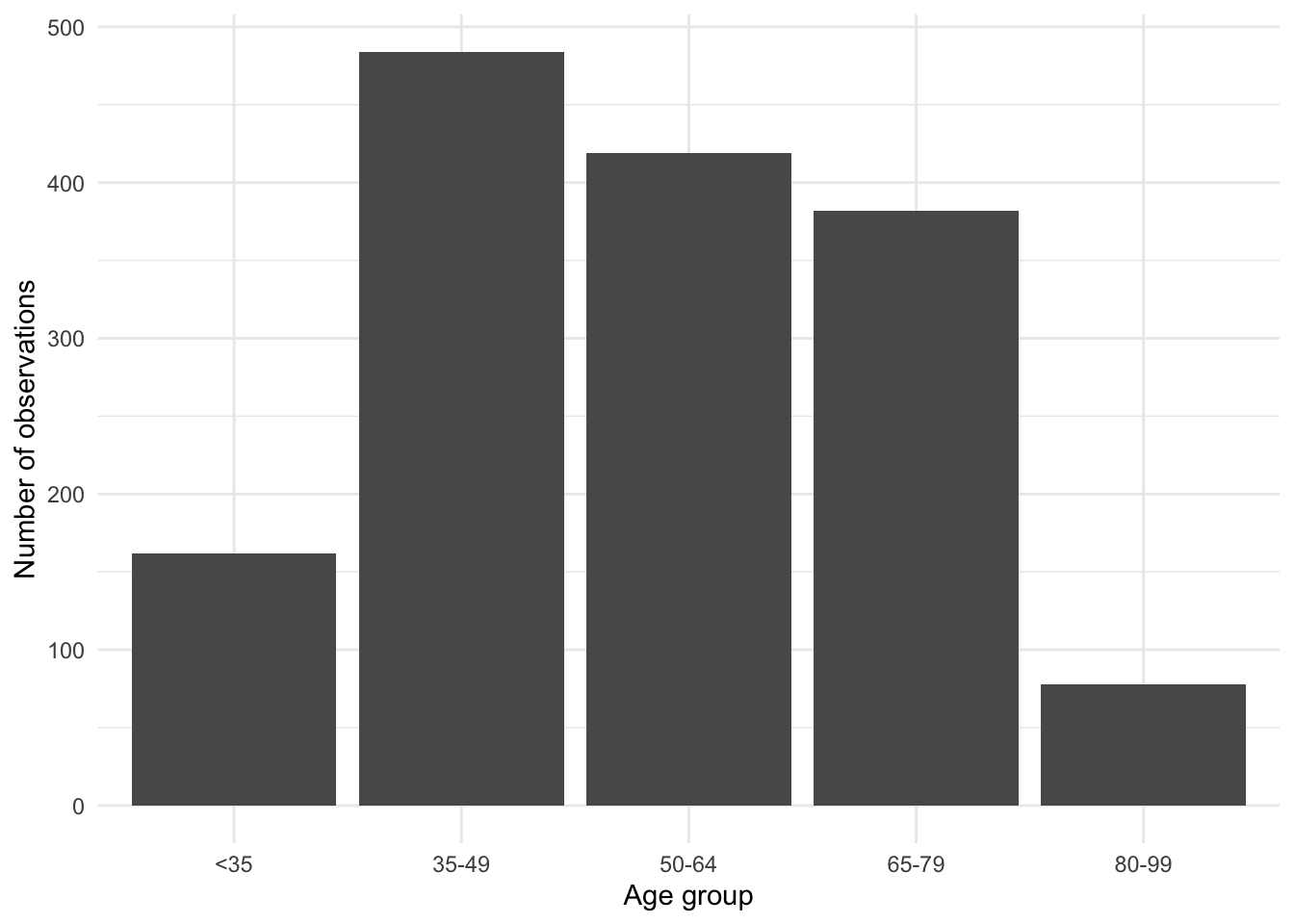

(a) Using geom_bar()

(b) Using count() and geom_col()

Figure 5.3: Distribution of age-groups in the 1997-2001 British Election Panel Study

The default axis label used by ggplot2 is the name of the relevant variable, so it is often useful to add more detail. We do this using labs() by specifying a variable and a name. In the case of Figure 5.3 (a) we have specified labels for the x-axis and y-axis.

By default, geom_bar() creates a count of the number of times each age-group appears in the dataset. It does this because the default statistical transformation—a “stat”—for geom_bar() is “count”, which saves us from having to create that statistic ourselves. But if we had already constructed a count (for instance, with beps |> count(age_group)), then we could specify a variable for the y-axis and then use geom_col() (Figure 5.3 (b)).

We may also like to consider various groupings of the data to get a different insight. For instance, we can use color to look at which party the respondent supports, by age-group (Figure 5.4 (a)).

beps |>
  ggplot(mapping = aes(x = age_group, fill = vote)) +
  geom_bar() +
  labs(x = "Age group", y = "Number of observations", fill = "Vote") +
  theme(legend.position = "bottom")

beps |>
  ggplot(mapping = aes(x = age_group, fill = vote)) +
  geom_bar(position = "dodge2") +
  labs(x = "Age group", y = "Number of observations", fill = "Vote") +
  theme(legend.position = "bottom")

(a) Using geom_bar()

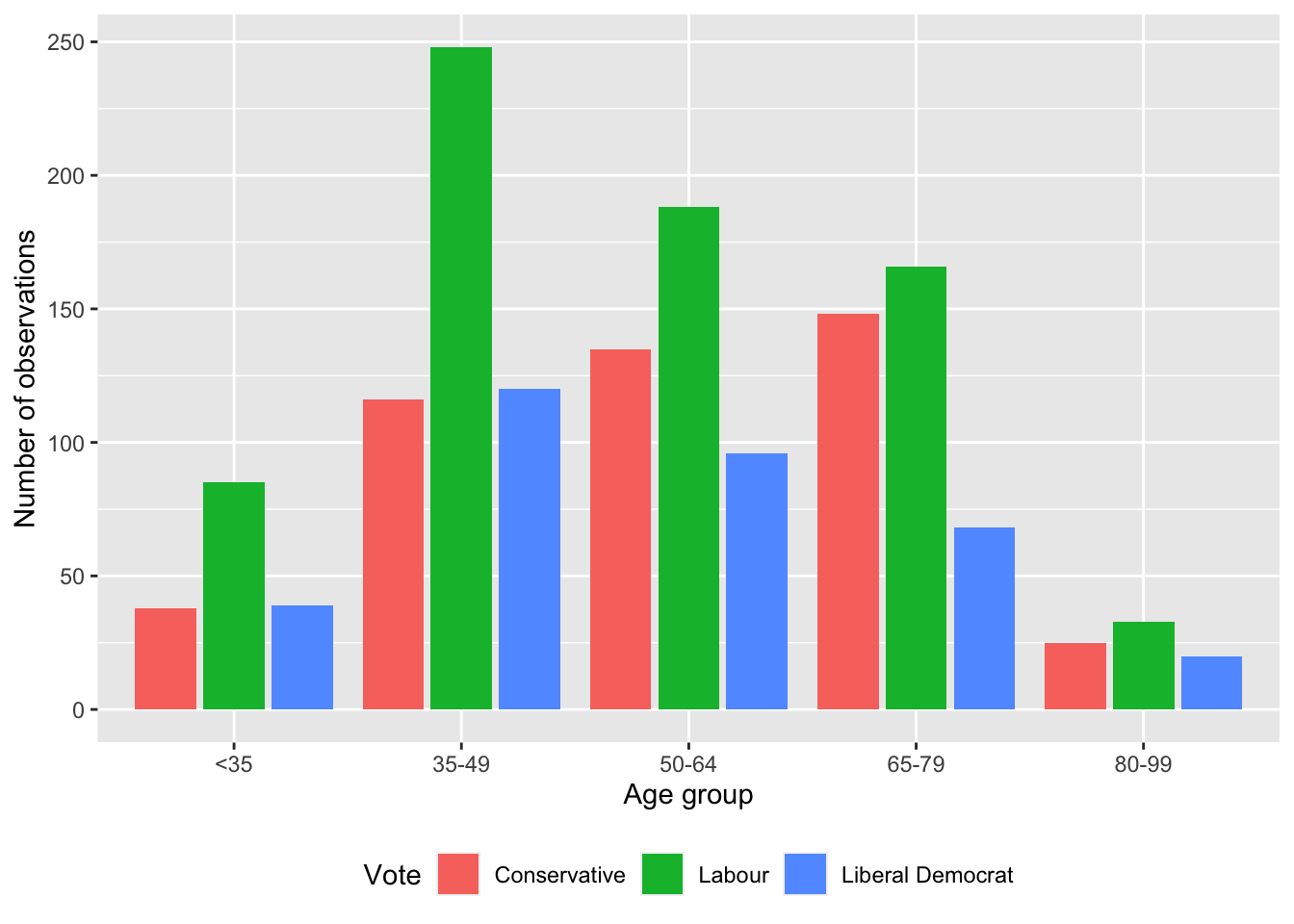
(b) Using geom_bar() with dodge2

Figure 5.4: Distribution of age-group, and vote preference, in the 1997-2001 British Election Panel Study

By default, these different groups are stacked, but they can be placed side by side with position = "dodge2" (Figure 5.4 (b)). (Using “dodge2” rather than “dodge” adds a little space between the bars.)

5.2.1.1 Themes

At this point, we may like to address the general look of the graph. There are various themes that are built into ggplot2. These include: theme_bw(), theme_classic(), theme_dark(), and theme_minimal(). A full list is available in the ggplot2 cheat sheet. We can use these themes by adding them as a layer (Figure 5.5). We could also install more themes from other packages, including ggthemes (Arnold 2021), and hrbrthemes (Rudis 2020). We could even build our own!

theme_bw <-
  beps |>
  ggplot(mapping = aes(x = age_group)) +
  geom_bar(position = "dodge") +
  theme_bw()

theme_classic <-
  beps |>
  ggplot(mapping = aes(x = age_group)) +
  geom_bar(position = "dodge") +
  theme_classic()

theme_dark <-
  beps |>
  ggplot(mapping = aes(x = age_group)) +
  geom_bar(position = "dodge") +
  theme_dark()

theme_minimal <-
  beps |>
  ggplot(mapping = aes(x = age_group)) +
  geom_bar(position = "dodge") +
  theme_minimal()

(theme_bw + theme_classic) / (theme_dark + theme_minimal)

Figure 5.5: Distribution of age-groups, and vote preference, in the 1997-2001 British Election Panel Study, illustrating different themes and the use of patchwork

In Figure 5.5 we use patchwork to bring together multiple graphs. To do this, after installing and loading the package, we assign the graph to a variable. We then use “+” to signal which should be next to each other, “/” to signal which should be on top, and use brackets to indicate precedence

5.2.1.2 Facets

We use facets to show variation, based on one or more variables (Wilkinson 2005, 219). Facets are especially useful when we have already used color to highlight variation in some other variable. For instance, we may be interested to explain vote, by age and gender (Figure 5.6). We rotate the x-axis with guides(x = guide_axis(angle = 90)) to avoid overlapping. We also change the position of the legend with theme(legend.position = "bottom").

beps |>
  ggplot(mapping = aes(x = age_group, fill = gender)) +
  geom_bar() +
  theme_minimal() +
  labs(
    x = "Age-group of respondent",
    y = "Number of respondents",
    fill = "Gender"
  ) +
  facet_wrap(vars(vote)) +
  guides(x = guide_axis(angle = 90)) +
  theme(legend.position = "bottom")

Figure 5.6: Distribution of age-group by gender, and vote preference, in the 1997-2001 British Election Panel Study

We could change facet_wrap() to wrap vertically instead of horizontally with dir = "v". Alternatively, we could specify a few rows, say nrow = 2, or a number of columns, say ncol = 2.

By default, both facets will have the same x-axis and y-axis. We could enable both facets to have different scales with scales = "free", or just the x-axis with scales = "free_x", or just the y-axis with scales = "free_y" (Figure 5.7).

beps |>
  ggplot(mapping = aes(x = age_group, fill = gender)) +
  geom_bar() +
  theme_minimal() +
  labs(
    x = "Age-group of respondent",
    y = "Number of respondents",
    fill = "Gender"
  ) +
  facet_wrap(vars(vote), scales = "free") +
  guides(x = guide_axis(angle = 90)) +
  theme(legend.position = "bottom")

Figure 5.7: Distribution of age-group by gender, and vote preference, in the 1997-2001 British Election Panel Study

Finally, we can change the labels of the facets using labeller() (Figure 5.8).

new_labels <- 
  c("0" = "No knowledge", "1" = "Low knowledge",
    "2" = "Moderate knowledge", "3" = "High knowledge")

beps |>
  ggplot(mapping = aes(x = age_group, fill = vote)) +
  geom_bar() +
  theme_minimal() +
  labs(
    x = "Age-group of respondent",
    y = "Number of respondents",
    fill = "Voted for"
  ) +
  facet_wrap(
    vars(political_knowledge),
    scales = "free",
    labeller = labeller(political_knowledge = new_labels)
  ) +
  guides(x = guide_axis(angle = 90)) +
  theme(legend.position = "bottom")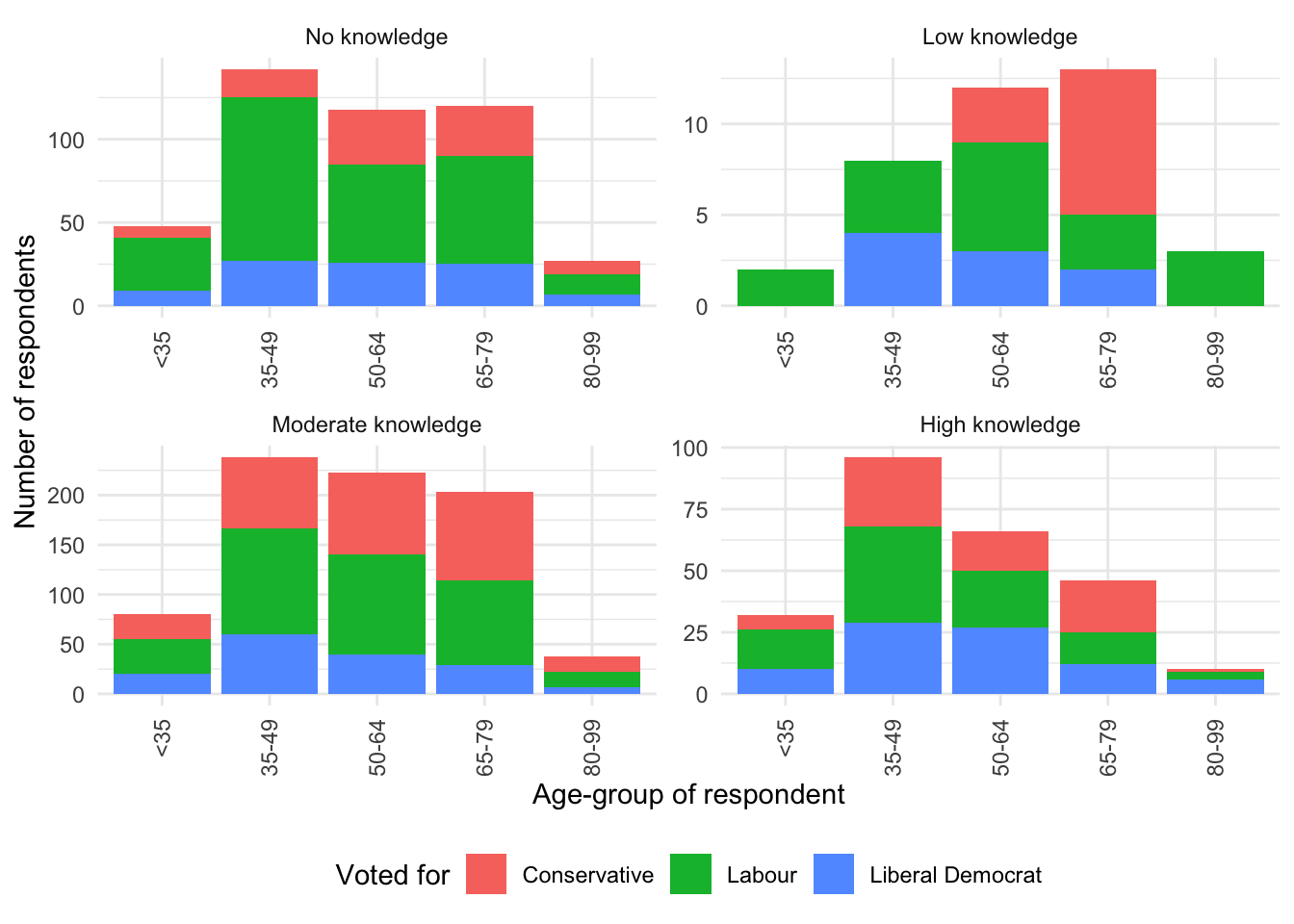

Figure 5.8: Distribution of age-group by political knowledge, and vote preference, in the 1997-2001 British Election Panel Study

We now have three ways to combine multiple graphs: sub-figures, facets, and patchwork. They are useful in different circumstances:

  • sub-figures—which we covered in Chapter 3—for when we are considering different variables;
  • facets for when we are considering a categorical variable; and
  • patchwork for when we are interested in bringing together entirely different graphs.

5.2.1.3 Colors

We now turn to the colors used in the graph. There are a variety of different ways to change the colors. The many palettes available from RColorBrewer (Neuwirth 2022) can be specified using scale_fill_brewer(). In the case of viridis (Garnier et al. 2021) we can specify the palettes using scale_fill_viridis_d(). Additionally, viridis is particularly focused on color-blind palettes (Figure 5.9). Neither RColorBrewer nor viridis need to be explicitly installed or loaded because ggplot2, which is part of the tidyverse, takes care of that for us.

Shoulders of giants

The name of the “brewer” palette refers to Cindy Brewer (Miller 2014). After earning a PhD in Geography from Michigan State University in 1991, she joined San Diego State University as an assistant professor, moving to Pennsylvania State University in 1994, where she was promoted to full professor in 2007. One of her best-known books is Designing Better Maps: A Guide for GIS Users (Brewer 2015). In 2019 she became only the ninth person to have been awarded the O. M. Miller Cartographic Medal since it was established in 1968.

# Panel (a)
beps |>
  ggplot(mapping = aes(x = age_group, fill = vote)) +
  geom_bar() +
  theme_minimal() +
  labs(x = "Age-group", y = "Number", fill = "Voted for") +
  theme(legend.position = "bottom") +
  scale_fill_brewer(palette = "Blues")

# Panel (b)
beps |>
  ggplot(mapping = aes(x = age_group, fill = vote)) +
  geom_bar() +
  theme_minimal() +
  labs(x = "Age-group", y = "Number", fill = "Voted for") +
  theme(legend.position = "bottom") +
  scale_fill_brewer(palette = "Set1")

# Panel (c)
beps |>
  ggplot(mapping = aes(x = age_group, fill = vote)) +
  geom_bar() +
  theme_minimal() +
  labs(x = "Age-group", y = "Number", fill = "Voted for") +
  theme(legend.position = "bottom") +
  scale_fill_viridis_d()

# Panel (d)
beps |>
  ggplot(mapping = aes(x = age_group, fill = vote)) +
  geom_bar() +
  theme_minimal() +
  labs(x = "Age-group", y = "Number", fill = "Voted for") +
  theme(legend.position = "bottom") +
  scale_fill_viridis_d(option = "magma")

(a) Brewer palette ‘Blues’

(b) Brewer palette ‘Set1’

(c) Viridis palette default

(d) Viridis palette ‘magma’

Figure 5.9: Distribution of age-group and vote preference, in the 1997-2001 British Election Panel Study, illustrating different colors

In addition to using pre-built palettes, we could build our own palette. That said, color is something to be considered with care. It should be used to increase the amount of information that is communicated (Cleveland [1985] 1994). Color should not be added to graphs unnecessarily—that is to say, it should play some role. Typically, that role is to distinguish different groups, which implies making the colors dissimilar. Color may also be appropriate if there is some relationship between the color and the variable. For instance, if making a graph of the price of mangoes and raspberries, then it could help the reader decode the information if the colors were yellow and red, respectively (Franconeri et al. 2021, 121).

5.2.2 Scatterplots

We are often interested in the relationship between two numeric or continuous variables. We can use scatterplots to show this. A scatterplot may not always be the best choice, but it is rarely a bad one (Weissgerber et al. 2015). Some consider it the most versatile and useful graph option (Friendly and Wainer 2021, 121). To illustrate scatterplots, we install and load WDI and then use that to download some economic indicators from the World Bank. In particular, we use WDIsearch() to find the unique key that we need to pass to WDI() to facilitate the download.

Oh, you think we have good data on that!

From OECD (2014, 15) Gross Domestic Product (GDP) “combines in a single figure, and with no double counting, all the output (or production) carried out by all the firms, non-profit institutions, government bodies and households in a given country during a given period, regardless of the type of goods and services produced, provided that the production takes place within the country’s economic territory.” The modern concept was developed by the twentieth century economist Simon Kuznets and is widely used and reported. There is a certain comfort in having a definitive and concrete single number to describe something as complicated as the economic activity of a country. It is useful and informative that we have such summary statistics. But as with any summary statistic, its strength is also its weakness. A single number necessarily loses information about constituent components, and disaggregated differences can be important (Moyer and Dunn 2020). It highlights short term economic progress over longer term improvements. And “the quantitative definiteness of the estimates makes it easy to forget their dependence upon imperfect data and the consequently wide margins of possible error to which both totals and components are liable” (Kuznets, Epstein, and Jenks 1941, xxvi). Summary measures of economic performance shows only one side of a country’s economy. While there are many strengths there are also well-known areas where GDP is weak.

WDIsearch("gdp growth")
WDIsearch("inflation")
WDIsearch("population, total")
WDIsearch("Unemployment, total")
world_bank_data <-
  WDI(
    indicator =
      c("FP.CPI.TOTL.ZG", "NY.GDP.MKTP.KD.ZG", "SP.POP.TOTL","SL.UEM.TOTL.NE.ZS"),
    country = c("AU", "ET", "IN", "US")
  )

We may like to change the variable names to be more meaningful, and only keep those that we need.

world_bank_data <-
  world_bank_data |>
  rename(
    inflation = FP.CPI.TOTL.ZG,
    gdp_growth = NY.GDP.MKTP.KD.ZG,
    population = SP.POP.TOTL,
    unem_rate = SL.UEM.TOTL.NE.ZS
  ) |>
  select(country, year, inflation, gdp_growth, population, unem_rate)

head(world_bank_data)
# A tibble: 6 × 6
  country    year inflation gdp_growth population unem_rate
  <chr>     <dbl>     <dbl>      <dbl>      <dbl>     <dbl>
1 Australia  1960     3.73       NA      10276477        NA
2 Australia  1961     2.29        2.48   10483000        NA
3 Australia  1962    -0.319       1.29   10742000        NA
4 Australia  1963     0.641       6.22   10950000        NA
5 Australia  1964     2.87        6.98   11167000        NA
6 Australia  1965     3.41        5.98   11388000        NA

To get started we can use geom_point() to make a scatterplot showing GDP growth and inflation, by country (Figure 5.10 (a)).

# Panel (a)
world_bank_data |>
  ggplot(mapping = aes(x = gdp_growth, y = inflation, color = country)) +
  geom_point()

# Panel (b)
world_bank_data |>
  ggplot(mapping = aes(x = gdp_growth, y = inflation, color = country)) +
  geom_point() +
  theme_minimal() +
  labs(x = "GDP growth", y = "Inflation", color = "Country")

(a) Default settings

(b) With the addition of a theme and labels

Figure 5.10: Relationship between inflation and GDP growth for Australia, Ethiopia, India, and the United States

As with bar charts, we can change the theme, and update the labels (Figure 5.10 (b)).

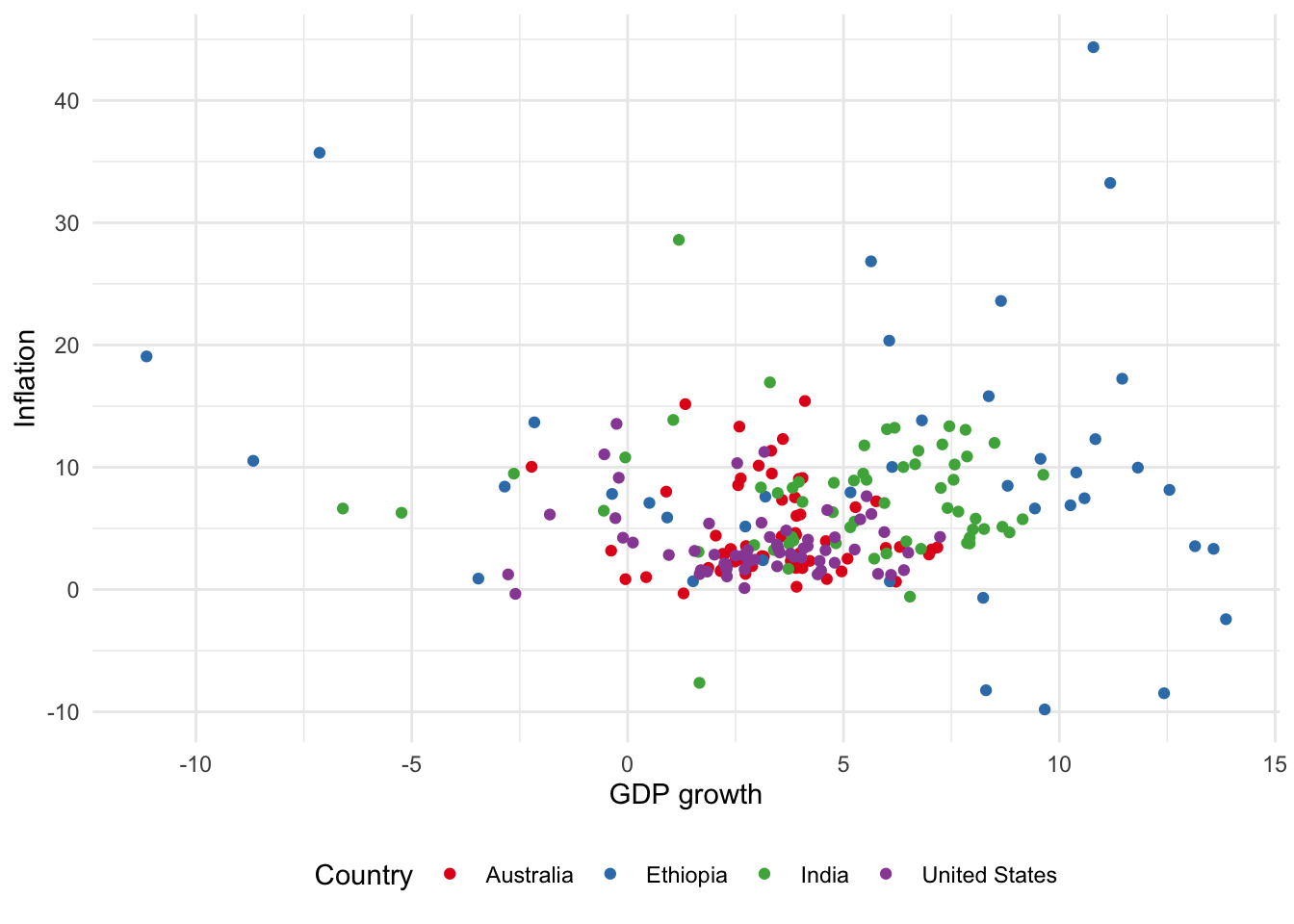
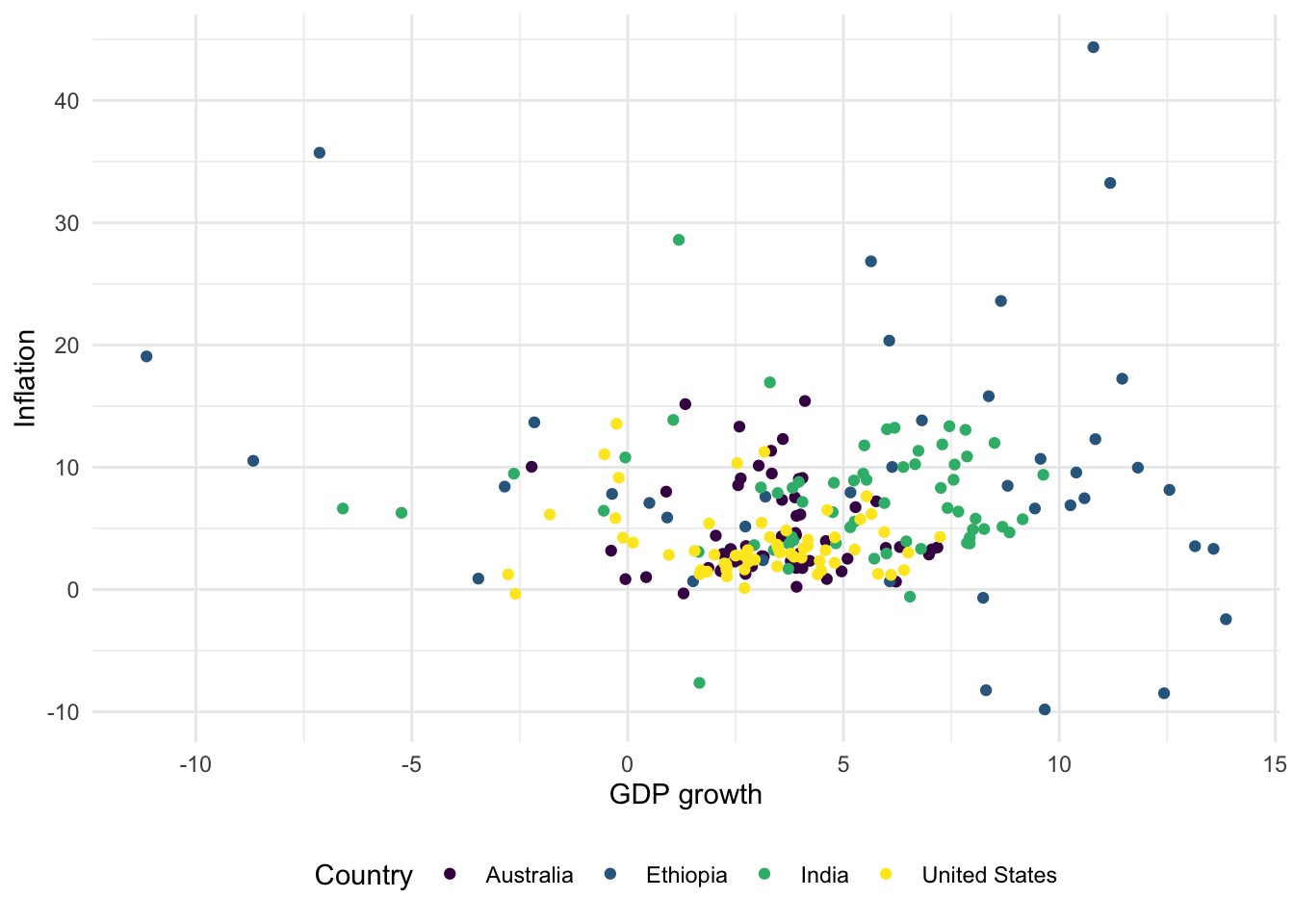
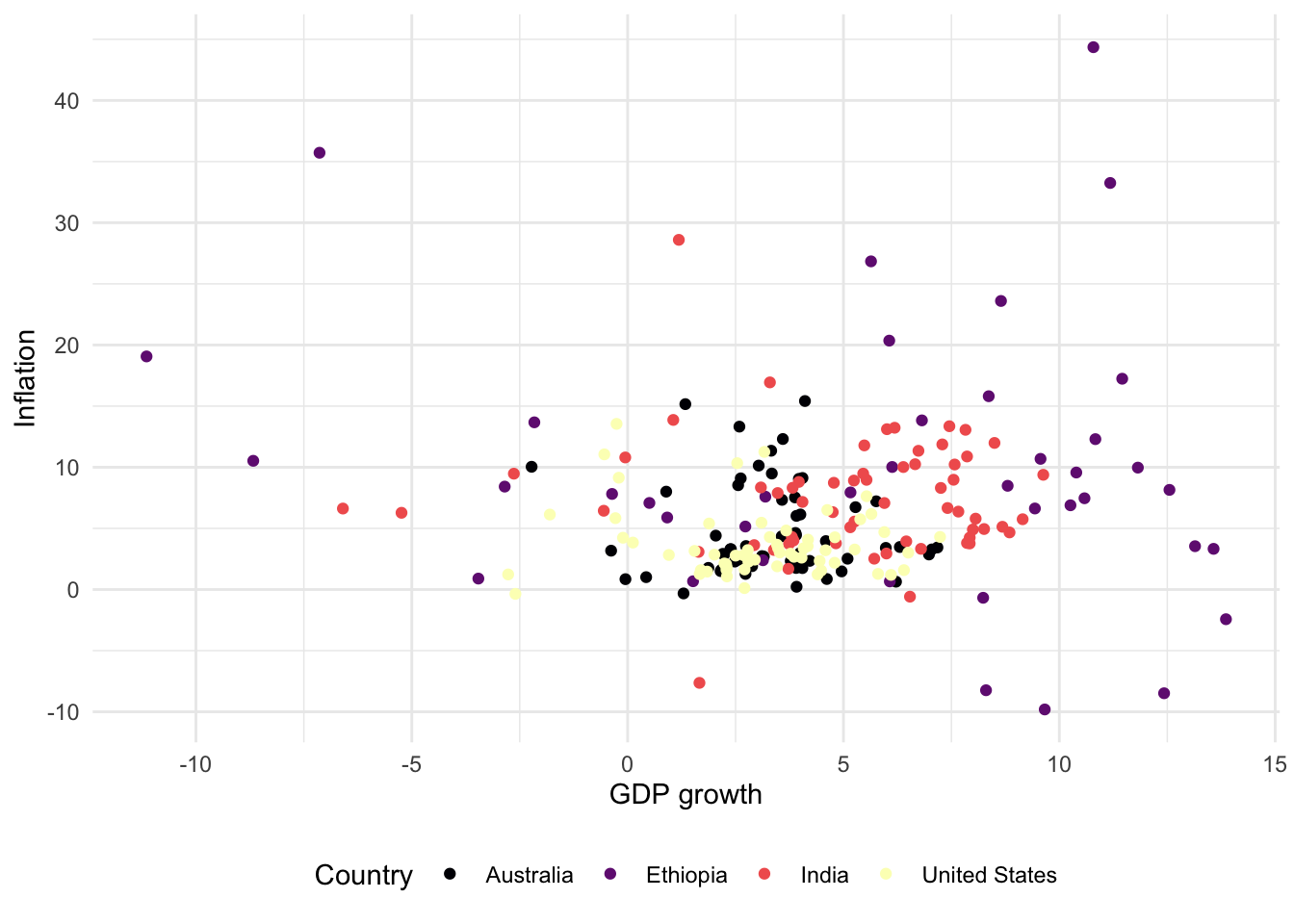
For scatterplots we use “color” instead of “fill”, as we did for bar charts, because they use dots rather than bars. This also then slightly affects how we change the palette (Figure 5.11). That said, with particular types of dots, for instance shape = 21, it is possible to have both fill and color aesthetics.

# Panel (a)
world_bank_data |>
  ggplot(aes(x = gdp_growth, y = inflation, color = country)) +
  geom_point() +
  theme_minimal() +
  labs(x = "GDP growth", y = "Inflation", color = "Country") +
  theme(legend.position = "bottom") +
  scale_color_brewer(palette = "Blues")

# Panel (b)
world_bank_data |>
  ggplot(aes(x = gdp_growth, y = inflation, color = country)) +
  geom_point() +
  theme_minimal() +
  labs(x = "GDP growth",  y = "Inflation", color = "Country") +
  theme(legend.position = "bottom") +
  scale_color_brewer(palette = "Set1")

# Panel (c)
world_bank_data |>
  ggplot(aes(x = gdp_growth, y = inflation, color = country)) +
  geom_point() +
  theme_minimal() +
  labs(x = "GDP growth",  y = "Inflation", color = "Country") +
  theme(legend.position = "bottom") +
  scale_colour_viridis_d()

# Panel (d)
world_bank_data |>
  ggplot(aes(x = gdp_growth, y = inflation, color = country)) +
  geom_point() +
  theme_minimal() +
  labs(x = "GDP growth",  y = "Inflation", color = "Country") +
  theme(legend.position = "bottom") +
  scale_colour_viridis_d(option = "magma")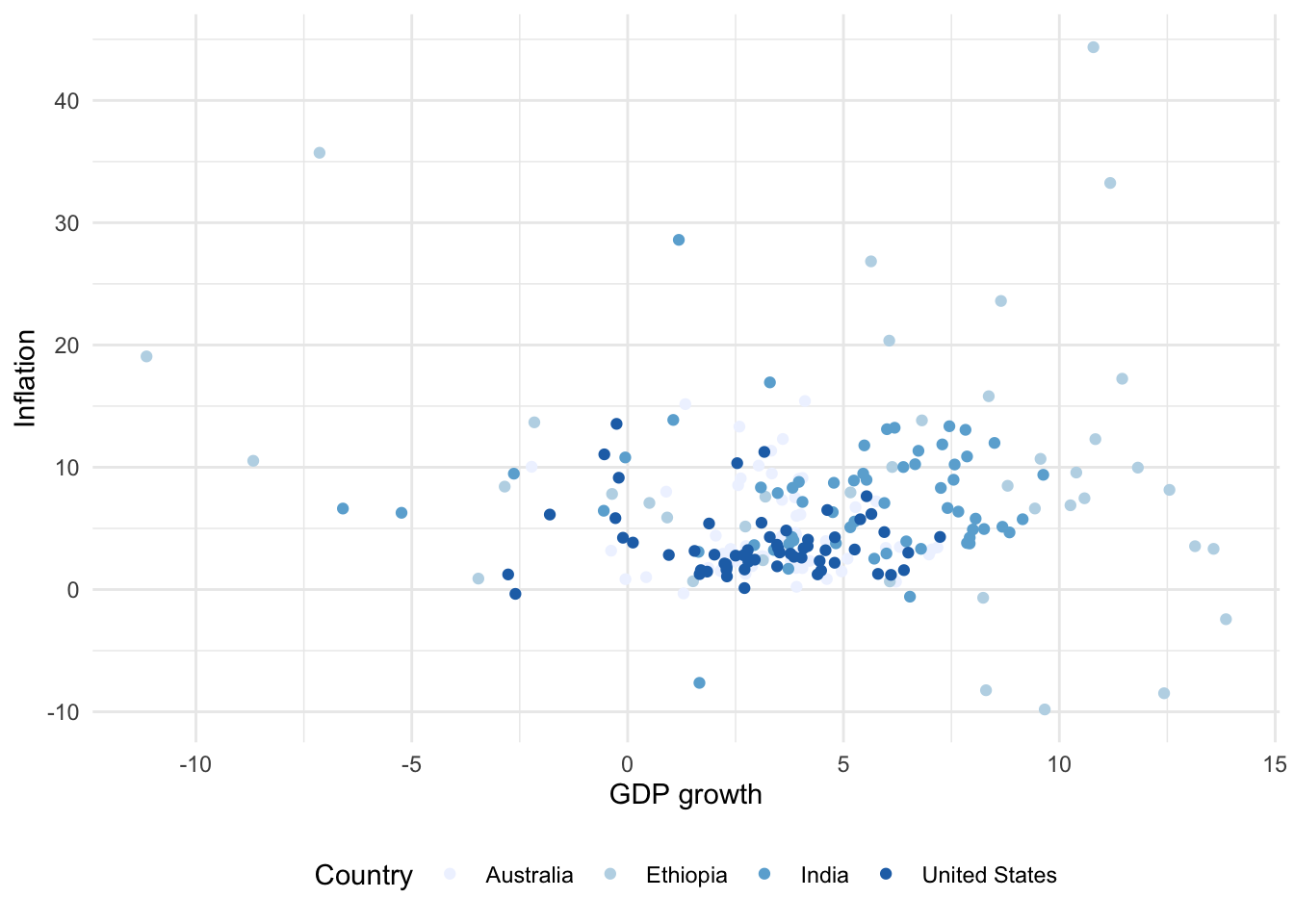

(a) Brewer palette ‘Blues’

(b) Brewer palette ‘Set1’

(c) Viridis palette default

(d) Viridis palette ‘magma’

Figure 5.11: Relationship between inflation and GDP growth for Australia, Ethiopia, India, and the United States

The points of a scatterplot sometimes overlap. We can address this situation in a variety of ways (Figure 5.12):

  1. Adding a degree of transparency to our dots with “alpha” (Figure 5.12 (a)). The value for “alpha” can vary between 0, which is fully transparent, and 1, which is completely opaque.
  2. Adding a small amount of noise, which slightly moves the points, using geom_jitter() (Figure 5.12 (b)). By default, the movement is uniform in both directions, but we can specify which direction movement occurs with “width” or “height”. The decision between these two options turns on the degree to which accuracy matters, and the number of points: it is often useful to use geom_jitter() when you want to highlight the relative density of points and not necessarily the exact value of individual points. When using geom_jitter() it is a good idea to set a seed, as introduced in Chapter 2, for reproducibility.
set.seed(853)

# Panel (a)
world_bank_data |>
  ggplot(aes(x = gdp_growth, y = inflation, color = country )) +
  geom_point(alpha = 0.5) +
  theme_minimal() +
  labs(x = "GDP growth", y = "Inflation", color = "Country")

# Panel (b)
world_bank_data |>
  ggplot(aes(x = gdp_growth, y = inflation, color = country)) +
  geom_jitter(width = 1, height = 1) +
  theme_minimal() +
  labs(x = "GDP growth", y = "Inflation", color = "Country")

(a) Changing the alpha setting

(b) Using jitter

Figure 5.12: Relationship between inflation and GDP growth for Australia, Ethiopia, India, and the United States

We often use scatterplots to illustrate a relationship between two continuous variables. It can be useful to add a “summary” line using geom_smooth() (Figure 5.13). We can specify the relationship using “method”, change the color with “color”, and add or remove standard errors with “se”. A commonly used “method” is lm, which computes and plots a simple linear regression line similar to using the lm() function. Using geom_smooth() adds a layer to the graph, and so it inherits aesthetics from ggplot(). For instance, that is why we have one line for each country in Figure 5.13 (a) and Figure 5.13 (b). We could overwrite that by specifying a particular color (Figure 5.13 (c)). There are situation where other types of fitted lines such as splines might be preferred.

# Panel (a)
world_bank_data |>
  ggplot(aes(x = gdp_growth, y = inflation, color = country)) +
  geom_jitter() +
  geom_smooth() +
  theme_minimal() +
  labs(x = "GDP growth", y = "Inflation", color = "Country")

# Panel (b)
world_bank_data |>
  ggplot(aes(x = gdp_growth, y = inflation, color = country)) +
  geom_jitter() +
  geom_smooth(method = lm, se = FALSE) +
  theme_minimal() +
  labs(x = "GDP growth", y = "Inflation", color = "Country")

# Panel (c)
world_bank_data |>
  ggplot(aes(x = gdp_growth, y = inflation, color = country)) +
  geom_jitter() +
  geom_smooth(method = lm, color = "black", se = FALSE) +
  theme_minimal() +
  labs(x = "GDP growth", y = "Inflation", color = "Country")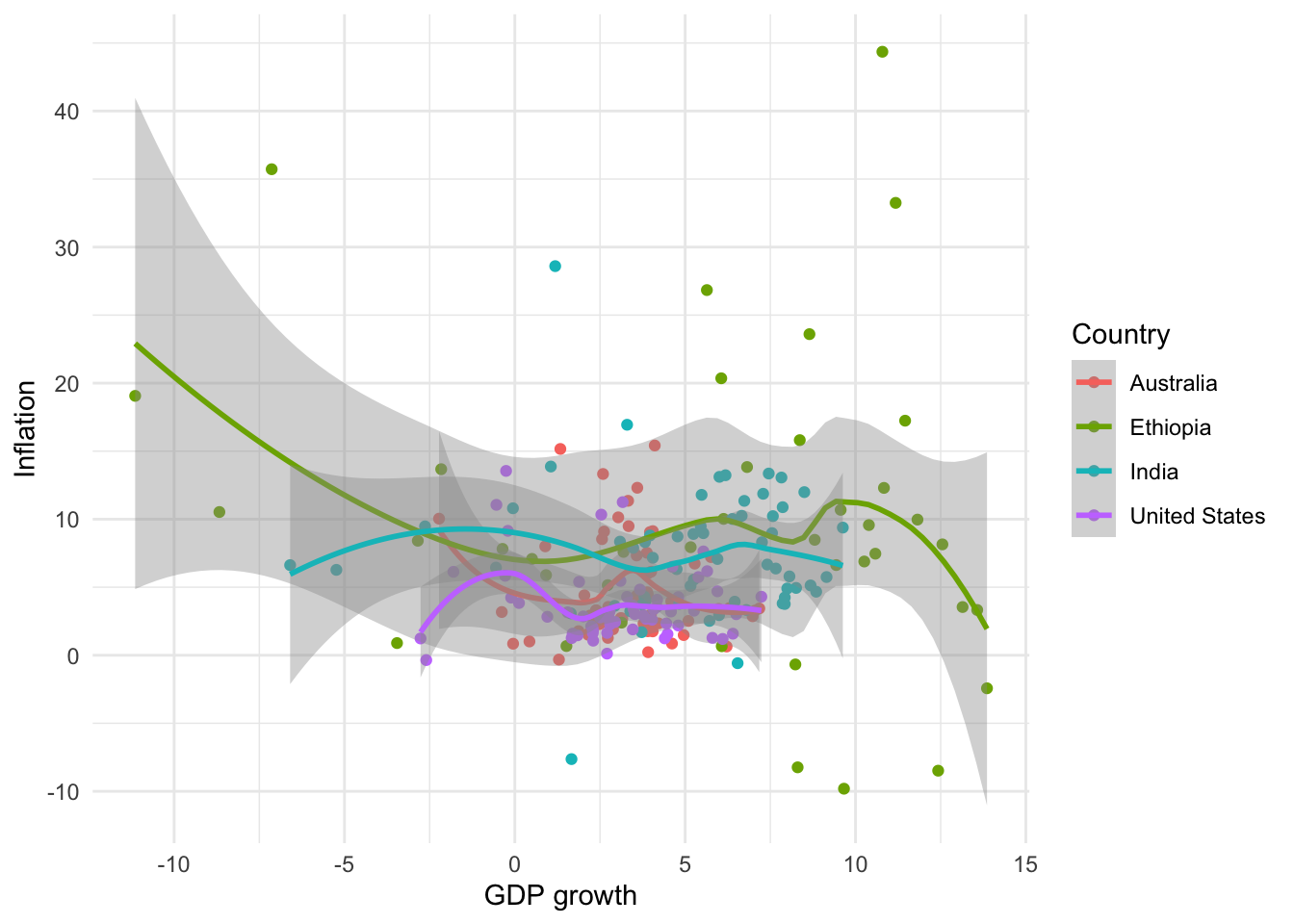

(a) Default line of best fit

(b) Specifying a linear relationship

(c) Specifying only one color

Figure 5.13: Relationship between inflation and GDP growth for Australia, Ethiopia, India, and the United States

5.2.3 Line plots

We can use a line plot when we have variables that should be joined together, for instance, an economic time series. We will continue with the dataset from the World Bank and focus on GDP growth in the United States using geom_line() (Figure 5.14 (a)). The source of the data can be added to the graph using “caption” within labs().

# Panel (a)
world_bank_data |>
  filter(country == "United States") |>
  ggplot(mapping = aes(x = year, y = gdp_growth)) +
  geom_line() +
  theme_minimal() +
  labs(x = "Year", y = "GDP growth", caption = "Data source: World Bank.")

# Panel (b)
world_bank_data |>
  filter(country == "United States") |>
  ggplot(mapping = aes(x = year, y = gdp_growth)) +
  geom_step() +
  theme_minimal() +
  labs(x = "Year",y = "GDP growth", caption = "Data source: World Bank.")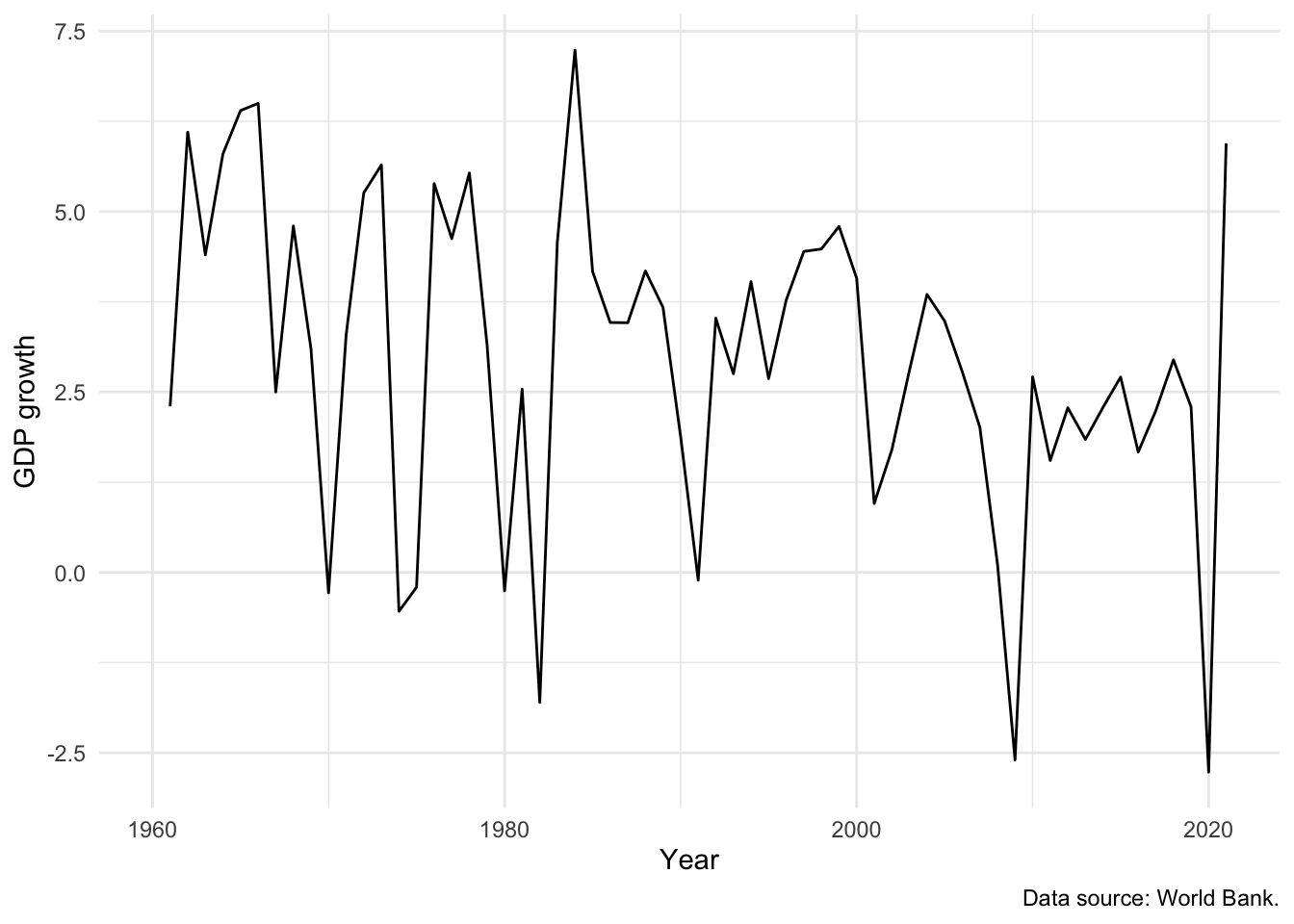

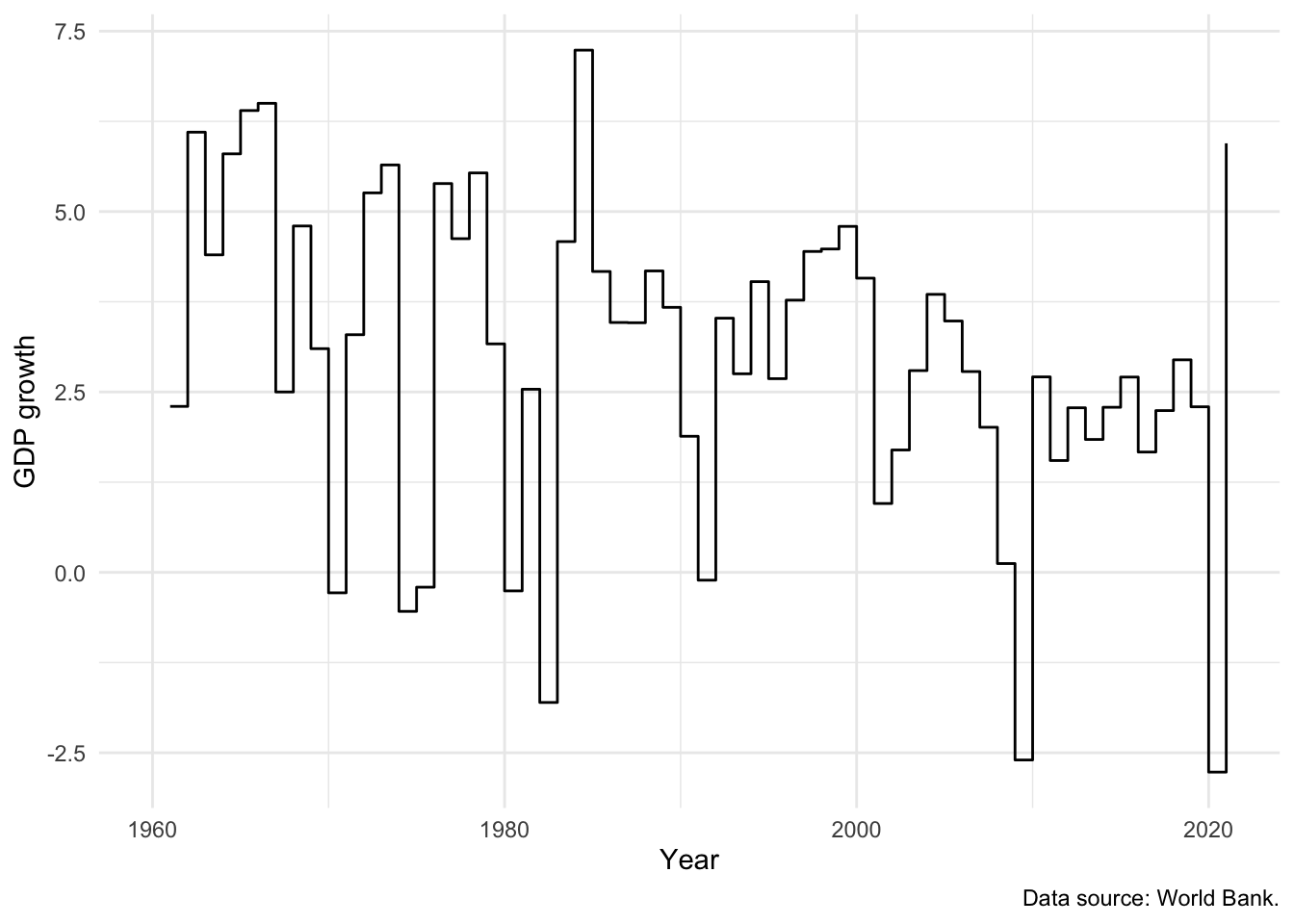
(a) Using a line plot

(b) Using a stairstep line plot

Figure 5.14: United States GDP growth (1961-2020)

We can use geom_step(), a slight variant of geom_line(), to focus attention on the change from year to year (Figure 5.14 (b)).

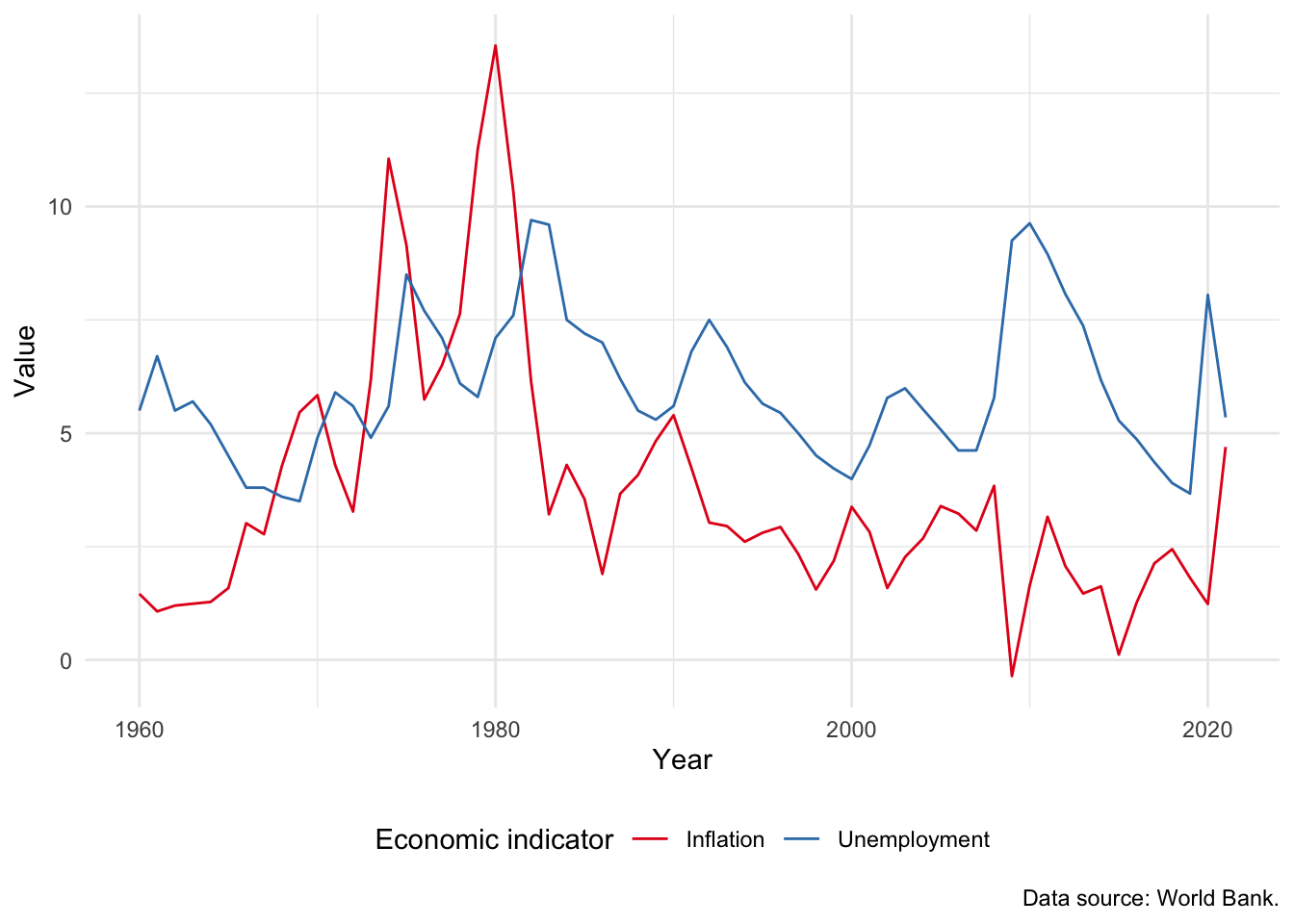
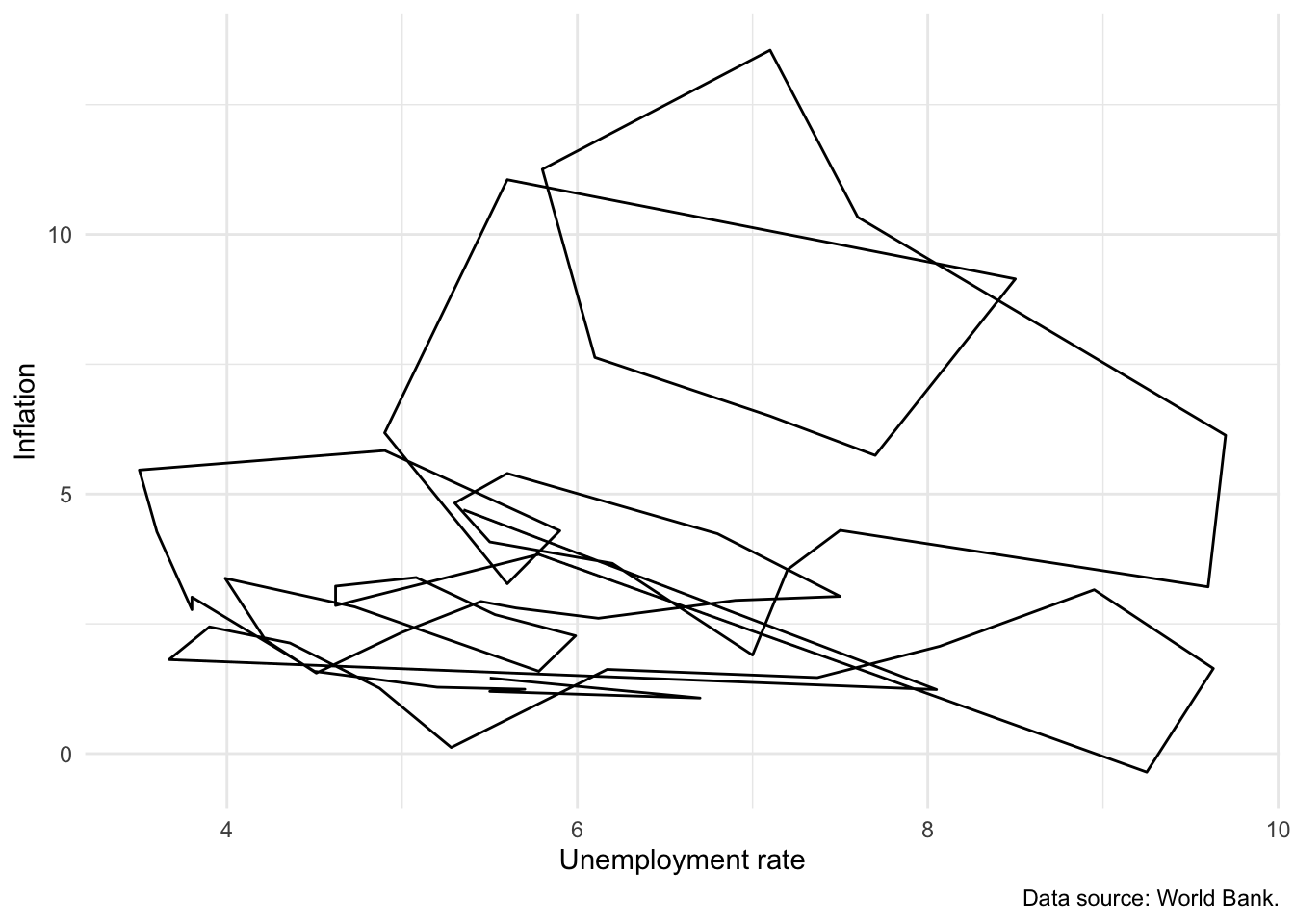
The Phillips curve is the name given to plot of the relationship between unemployment and inflation over time. An inverse relationship is sometimes found in the data, for instance in the United Kingdom between 1861 and 1957 (Phillips 1958). We have a variety of ways to investigate this relationship in our data, including:

  1. Adding a second line to our graph. For instance, we could add inflation (Figure 5.15 (a)). This requires us to use pivot_longer(), which is discussed in Online Appendix A, to ensure that the data are in a tidy format.
  2. Using geom_path() to link values in the order they appear in the dataset. In Figure 5.15 (b) we show a Phillips curve for the United States between 1960 and 2020. Figure 5.15 (b) does not appear to show any clear relationship between unemployment and inflation.
world_bank_data |>
  filter(country == "United States") |>
  select(-population, -gdp_growth) |>
  pivot_longer(
    cols = c("inflation", "unem_rate"),
    names_to = "series",
    values_to = "value"
  ) |>
  ggplot(mapping = aes(x = year, y = value, color = series)) +
  geom_line() +
  theme_minimal() +
  labs(
    x = "Year", y = "Value", color = "Economic indicator",
    caption = "Data source: World Bank."
  ) +
  scale_color_brewer(palette = "Set1", labels = c("Inflation", "Unemployment")) +
  theme(legend.position = "bottom")

world_bank_data |>
  filter(country == "United States") |>
  ggplot(mapping = aes(x = unem_rate, y = inflation)) +
  geom_path() +
  theme_minimal() +
  labs(
    x = "Unemployment rate", y = "Inflation",
    caption = "Data source: World Bank."
  )

(a) Comparing the two time series over time

(b) Plotting the two time series against each other

Figure 5.15: Unemployment and inflation for the United States (1960-2020)

5.2.4 Histograms

A histogram is useful to show the shape of the distribution of a continuous variable. The full range of the data values is split into intervals called “bins” and the histogram counts how many observations fall into which bin. In Figure 5.16 we examine the distribution of GDP in Ethiopia.

world_bank_data |>
  filter(country == "Ethiopia") |>
  ggplot(aes(x = gdp_growth)) +
  geom_histogram() +
  theme_minimal() +
  labs(
    x = "GDP growth",
    y = "Number of occurrences",
    caption = "Data source: World Bank."
  )

Figure 5.16: Distribution of GDP growth in Ethiopia (1960-2020)

The key component that determines the shape of a histogram is the number of bins. This can be specified in one of two ways (Figure 5.17):

  1. specifying the number of “bins” to include; or
  2. specifying their “binwidth”.
# Panel (a)
world_bank_data |>
  filter(country == "Ethiopia") |>
  ggplot(aes(x = gdp_growth)) +
  geom_histogram(bins = 5) +
  theme_minimal() +
  labs(
    x = "GDP growth",
    y = "Number of occurrences"
  )

# Panel (b)
world_bank_data |>
  filter(country == "Ethiopia") |>
  ggplot(aes(x = gdp_growth)) +
  geom_histogram(bins = 20) +
  theme_minimal() +
  labs(
    x = "GDP growth",
    y = "Number of occurrences"
  )

# Panel (c)
world_bank_data |>
  filter(country == "Ethiopia") |>
  ggplot(aes(x = gdp_growth)) +
  geom_histogram(binwidth = 2) +
  theme_minimal() +
  labs(
    x = "GDP growth",
    y = "Number of occurrences"
  )

# Panel (d)
world_bank_data |>
  filter(country == "Ethiopia") |>
  ggplot(aes(x = gdp_growth)) +
  geom_histogram(binwidth = 5) +
  theme_minimal() +
  labs(
    x = "GDP growth",
    y = "Number of occurrences"
  )

(a) Five bins

(b) 20 bins

(c) Binwidth of two

(d) Binwidth of five

Figure 5.17: Distribution of GDP growth in Ethiopia (1960-2020)

Histograms can be thought of as locally averaging data, and the number of bins affects how much of this occurs. When there are only two bins then there is a lot of smoothing, but we lose a lot of accuracy. Too few bins results in more bias, while too many bins results in more variance (Wasserman 2005, 303). Our decision as to the number of bins, or their width, is concerned with trying to balance bias and variance. This will depend on a variety of concerns including the subject matter and the goal (Cleveland [1985] 1994, 135). This is one of the reasons that Denby and Mallows (2009) consider histograms to be especially valuable as exploratory tools.

Finally, while we can use “fill” to distinguish between different types of observations, it can get quite messy. It is usually better to:

  1. trace the outline of the distribution with geom_freqpoly() (Figure 5.18 (a))
  2. build stack of dots with geom_dotplot() (Figure 5.18 (b)); or
  3. add transparency, especially if the differences are more stark (Figure 5.18 (c)).
# Panel (a)
world_bank_data |>
  ggplot(aes(x = gdp_growth, color = country)) +
  geom_freqpoly() +
  theme_minimal() +
  labs(
    x = "GDP growth", y = "Number of occurrences",
    color = "Country",
    caption = "Data source: World Bank."
  ) +
  scale_color_brewer(palette = "Set1")

# Panel (b)
world_bank_data |>
  ggplot(aes(x = gdp_growth, group = country, fill = country)) +
  geom_dotplot(method = "histodot") +
  theme_minimal() +
  labs(
    x = "GDP growth", y = "Number of occurrences",
    fill = "Country",
    caption = "Data source: World Bank."
  ) +
  scale_color_brewer(palette = "Set1")

# Panel (c)
world_bank_data |>
  filter(country %in% c("India", "United States")) |>
  ggplot(mapping = aes(x = gdp_growth, fill = country)) +
  geom_histogram(alpha = 0.5, position = "identity") +
  theme_minimal() +
  labs(
    x = "GDP growth", y = "Number of occurrences",
    fill = "Country",
    caption = "Data source: World Bank."
  ) +
  scale_color_brewer(palette = "Set1")

(a) Tracing the outline

(b) Using dots

(c) Adding transparency

Figure 5.18: Distribution of GDP growth across various countries (1960-2020)

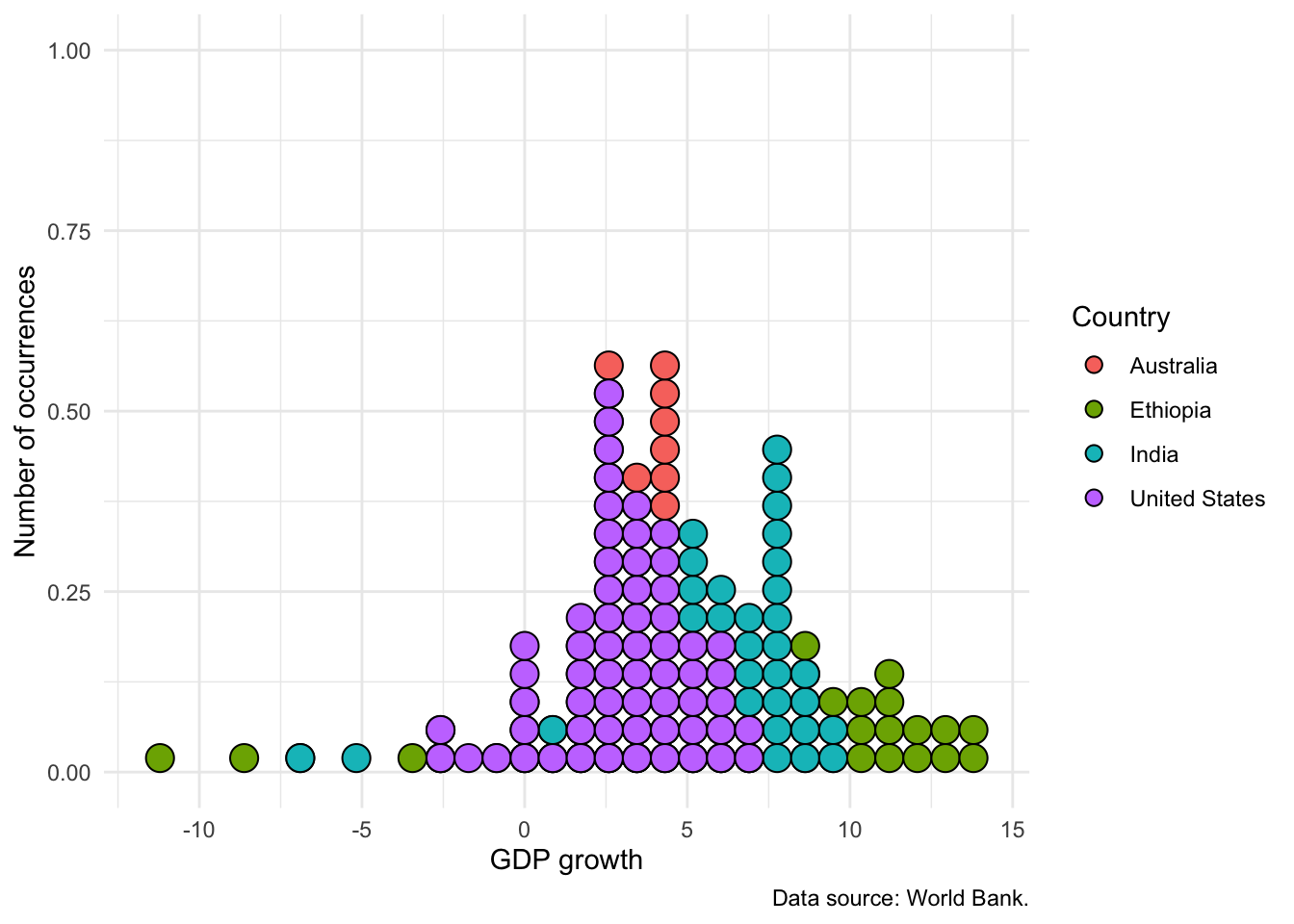
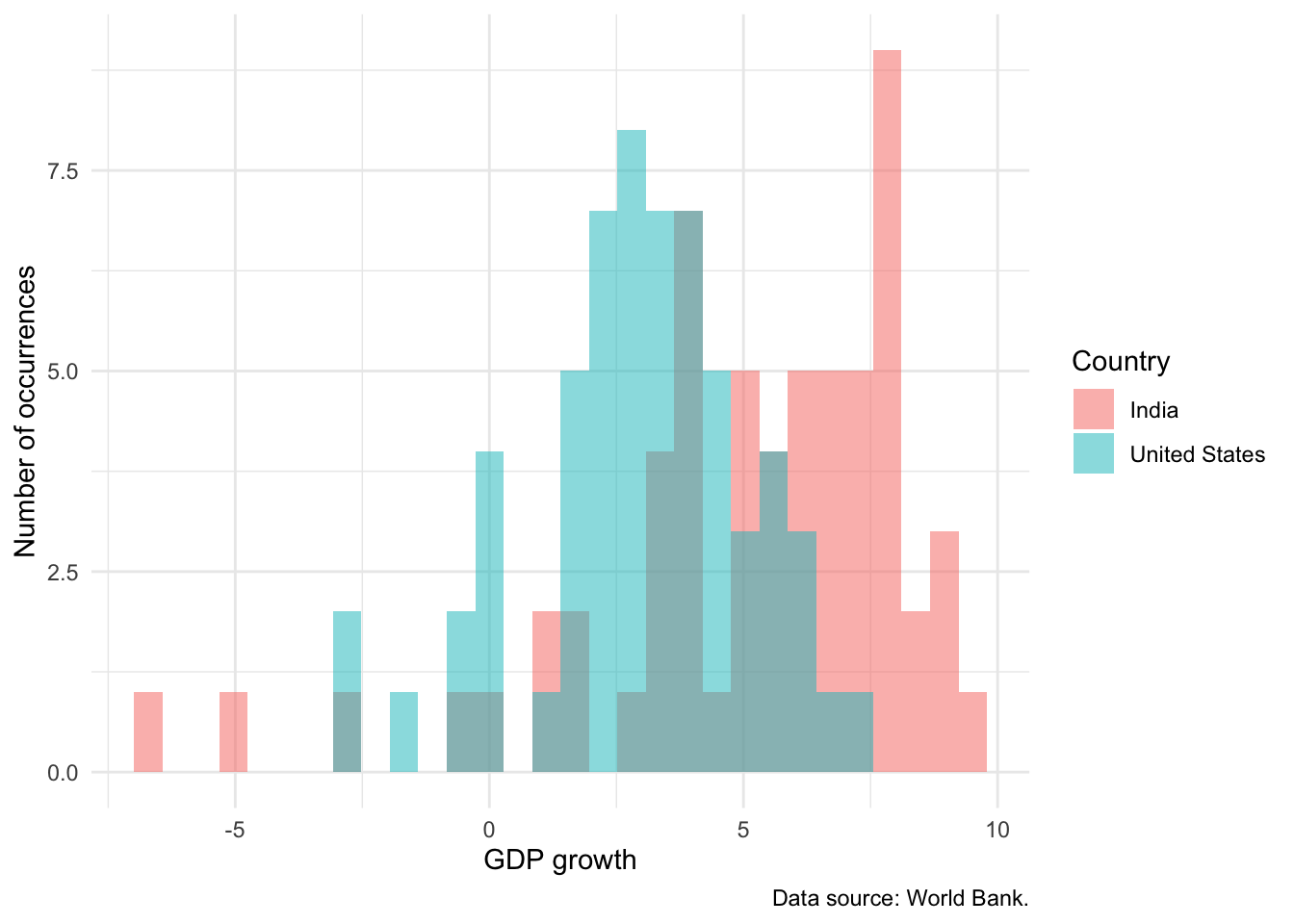
An interesting alternative to a histogram is the empirical cumulative distribution function (ECDF). The choice between this and a histogram is tends to be audience-specific. It may not appropriate for less-sophisticated audiences, but if the audience is quantitatively comfortable, then it can be a great choice because it does less smoothing than a histogram. We can build an ECDF with stat_ecdf(). For instance, Figure 5.19 shows an ECDF equivalent to Figure 5.16.

world_bank_data |>
  ggplot(mapping = aes(x = gdp_growth, color = country)) +
  stat_ecdf(geom = "point") +
  theme_minimal() +
  labs(
    x = "GDP growth", y = "Proportion", color = "Country",
    caption = "Data source: World Bank."
  ) + 
  theme(legend.position = "bottom")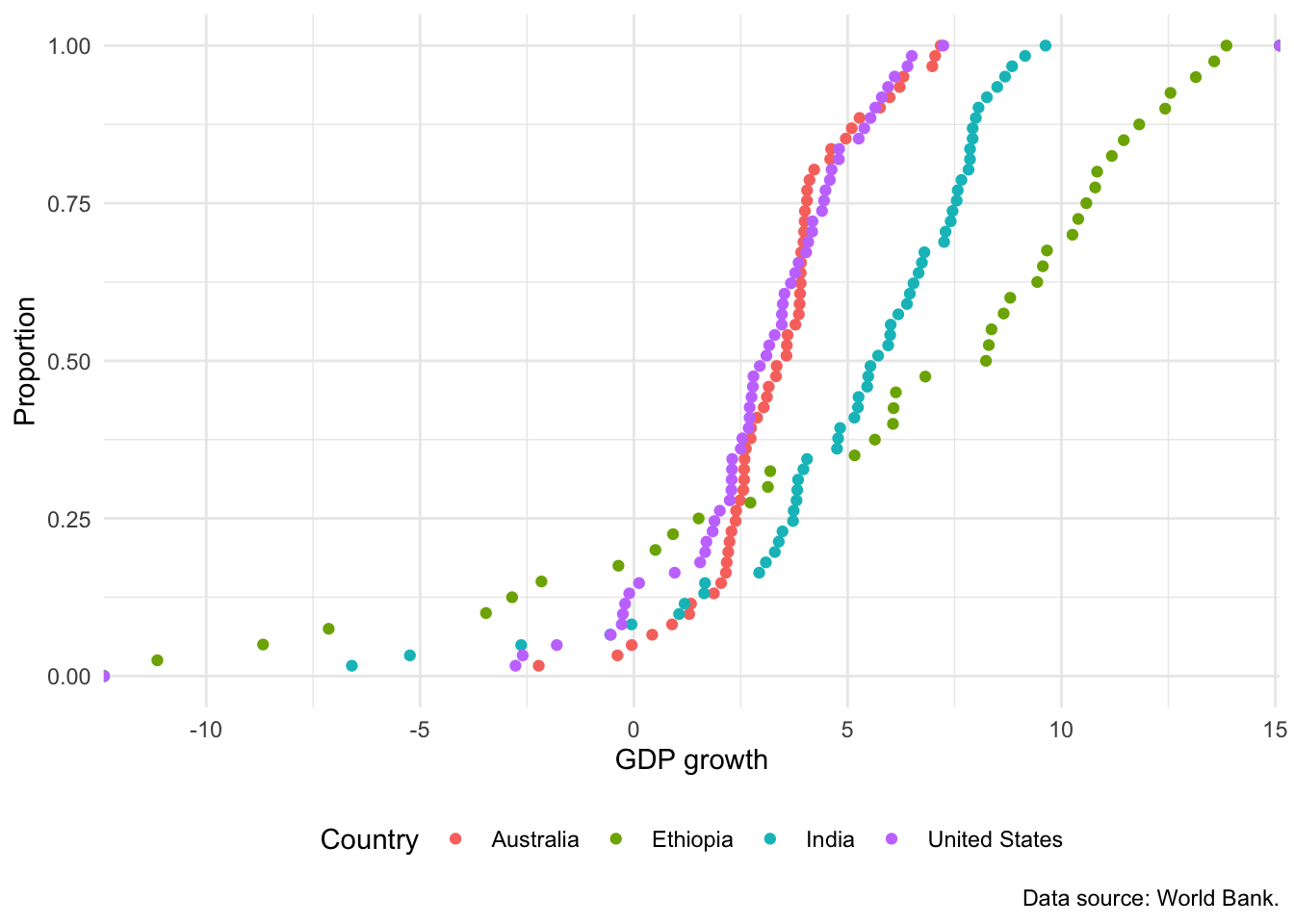

Figure 5.19: Distribution of GDP growth in four countries (1960-2020)

5.2.5 Boxplots

A boxplot typically shows five aspects: 1) the median, 2) the 25th, and 3) 75th percentiles. The fourth and fifth elements differ depending on specifics. One option is the minimum and maximum values. Another option is to determine the difference between the 75th and 25th percentiles, which is the interquartile range. The fourth and fifth elements are then \(1.5\times\mbox{IQR}\) from the 25th and 75th percentiles. That latter approach is used, by default, in geom_boxplot from ggplot2. Spear (1952, 166) introduced the notion of a chart that focused on the range and various summary statistics including the median and the range, while Tukey (1977) focused on which summary statistics and popularized it (Wickham and Stryjewski 2011).

One reason for using graphs is that they help us understand and embrace how complex our data are, rather than trying to hide and smooth it away (Armstrong 2022). One appropriate use case for boxplots is to compare the summary statistics of many variables at once, such as in Bethlehem et al. (2022). But boxplots alone are rarely the best choice because they hide the distribution of data, rather than show it. The same boxplot can apply to very different distributions. To see this, consider some simulated data from the beta distribution of two types. The first contains draws from two beta distributions: one that is right skewed and another that is left skewed. The second contains draws from a beta distribution with no skew, noting that \(\mbox{Beta}(1, 1)\) is equivalent to \(\mbox{Uniform}(0, 1)\).

set.seed(853)

number_of_draws <- 10000

both_left_and_right_skew <-
  c(
    rbeta(number_of_draws / 2, 5, 2),
    rbeta(number_of_draws / 2, 2, 5)
  )

no_skew <-
  rbeta(number_of_draws, 1, 1)

beta_distributions <-
  tibble(
    observation = c(both_left_and_right_skew, no_skew),
    source = c(
      rep("Left and right skew", number_of_draws),
      rep("No skew", number_of_draws)
    )
  )

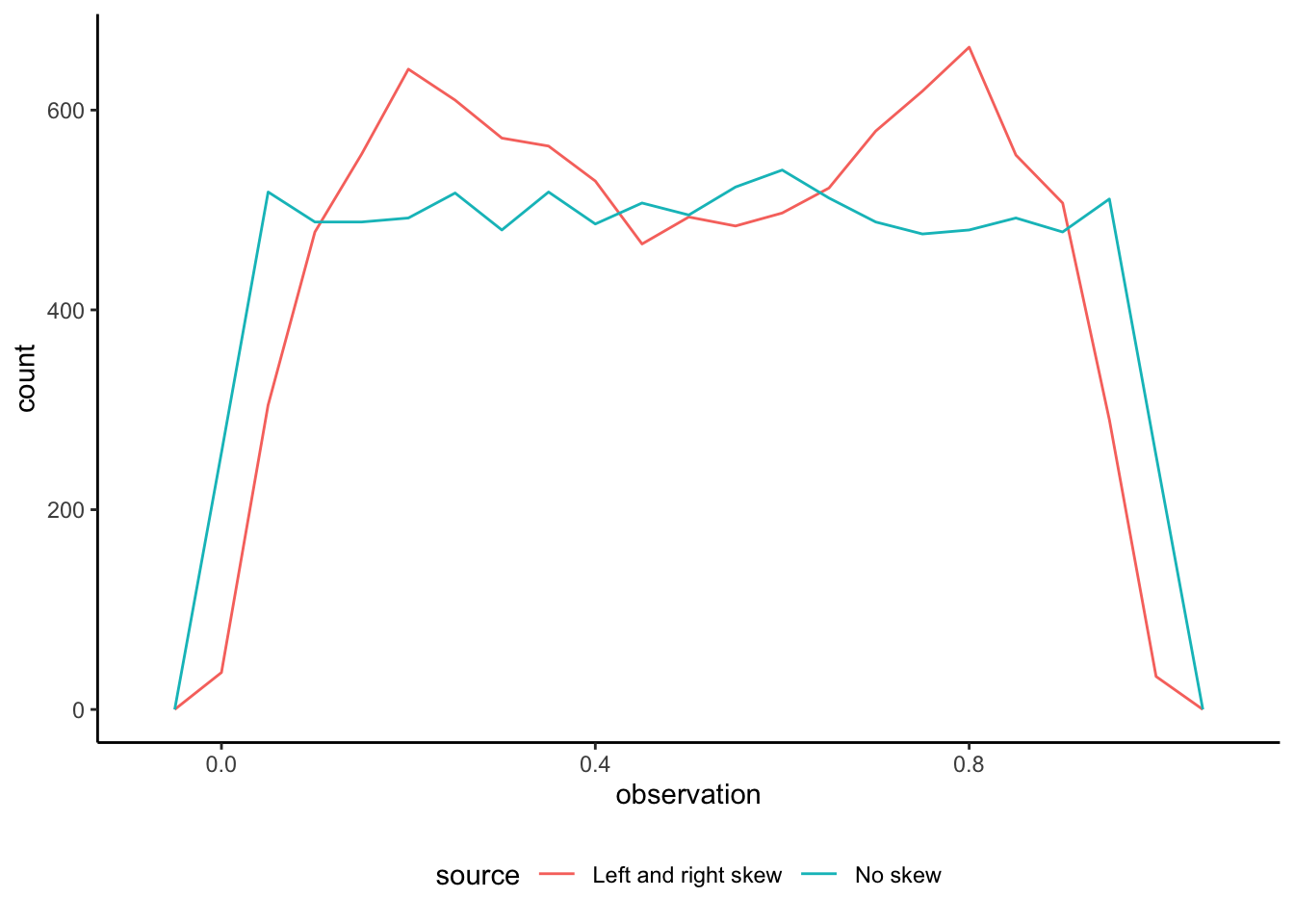
We can first compare the boxplots of the two series (Figure 5.20 (a)). But if we plot the actual data then we can see how different they are (Figure 5.20 (b)).

beta_distributions |>
  ggplot(aes(x = source, y = observation)) +
  geom_boxplot() +
  theme_classic()

beta_distributions |>
  ggplot(aes(x = observation, color = source)) +
  geom_freqpoly(binwidth = 0.05) +
  theme_classic() +
  theme(legend.position = "bottom")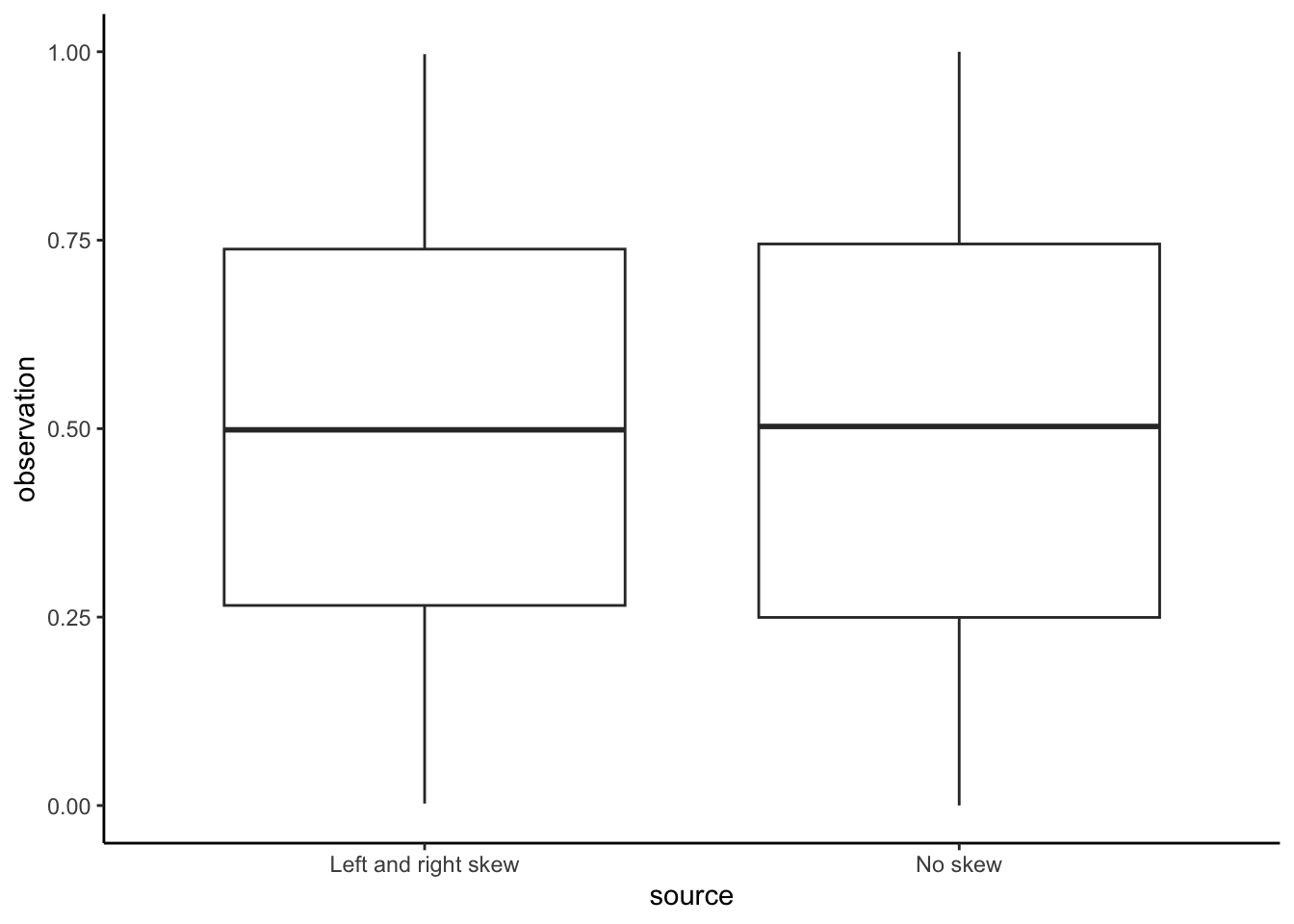

(a) Illustrated with a boxplot

(b) Actual data

Figure 5.20: Data drawn from beta distributions with different parameters

One way forward, if a boxplot is to be used, is to include the actual data as a layer on top of the boxplot. For instance, in Figure 5.21 we show the distribution of inflation across the four countries. The reason that this works well is that it shows the actual observations, as well as the summary statistics.

world_bank_data |>
  ggplot(mapping = aes(x = country, y = inflation)) +
  geom_boxplot() +
  geom_jitter(alpha = 0.3, width = 0.15, height = 0) +
  theme_minimal() +
  labs(
    x = "Country",
    y = "Inflation",
    caption = "Data source: World Bank."
  )

Figure 5.21: Distribution of inflation data for four countries (1960-2020)

5.3 Tables

Tables are an important part of telling a compelling story. Tables can communicate less information than a graph, but they do so at a high fidelity. They are especially useful to highlight a few specific values (Andersen and Armstrong 2021). In this book, we primarily use tables in three ways:

  1. To show an extract of the dataset.
  2. To communicate summary statistics.
  3. To display regression results.

5.3.1 Showing part of a dataset

We illustrate showing part of a dataset using kable() from knitr. We use the World Bank dataset that we downloaded earlier and focus on inflation, GDP growth, and population as unemployment data are not available for every year for every country.

world_bank_data <- 
  world_bank_data |> 
  select(-unem_rate)

To begin, after installing and loading knitr, we can display the first ten rows with the default kable() settings.

world_bank_data |>
  slice(1:10) |>
  kable()
country year inflation gdp_growth population
Australia 1960 3.7288136 NA 10276477
Australia 1961 2.2875817 2.482656 10483000
Australia 1962 -0.3194888 1.294611 10742000
Australia 1963 0.6410256 6.216107 10950000
Australia 1964 2.8662420 6.980061 11167000
Australia 1965 3.4055728 5.980438 11388000
Australia 1966 3.2934132 2.379040 11651000
Australia 1967 3.4782609 6.304945 11799000
Australia 1968 2.5210084 5.094034 12009000
Australia 1969 3.2786885 7.045584 12263000

To be able to cross-reference a table in the text, we need to add a table caption and label to the R chunk as shown in Section 3.2.6 of Chapter 3. We can also make the column names more informative with “col.names” and specify the number of digits to be displayed (Table 5.3).

```{r}
#| label: tbl-gdpfirst
#| message: false
#| tbl-cap: "A dataset of economic indicators for four countries"

world_bank_data |>
  slice(1:10) |>
  kable(
    col.names = c("Country", "Year", "Inflation", "GDP growth", "Population"),
    digits = 1
  )
```
Table 5.3: A dataset of economic indicators for four countries
Country Year Inflation GDP growth Population
Australia 1960 3.7 NA 10276477
Australia 1961 2.3 2.5 10483000
Australia 1962 -0.3 1.3 10742000
Australia 1963 0.6 6.2 10950000
Australia 1964 2.9 7.0 11167000
Australia 1965 3.4 6.0 11388000
Australia 1966 3.3 2.4 11651000
Australia 1967 3.5 6.3 11799000
Australia 1968 2.5 5.1 12009000
Australia 1969 3.3 7.0 12263000

5.3.2 Improving the formatting

When producing PDFs, the “booktabs” option makes a host of small changes to the default display and results in tables that look better (Table 5.4). (This should not have an effect for HTML output.) By default a small space will be added every five lines. We can additionally specify “linesep” to stop that.

world_bank_data |>
  slice(1:10) |>
  kable(
    col.names = c("Country", "Year", "Inflation", "GDP growth", "Population"),
    digits = 1,
    booktabs = TRUE,
    linesep = ""
  )
Table 5.4: First ten rows of a dataset of economic indicators for Australia, Ethiopia, India, and the United States
Country Year Inflation GDP growth Population
Australia 1960 3.7 NA 10276477
Australia 1961 2.3 2.5 10483000
Australia 1962 -0.3 1.3 10742000
Australia 1963 0.6 6.2 10950000
Australia 1964 2.9 7.0 11167000
Australia 1965 3.4 6.0 11388000
Australia 1966 3.3 2.4 11651000
Australia 1967 3.5 6.3 11799000
Australia 1968 2.5 5.1 12009000
Australia 1969 3.3 7.0 12263000

We can specify the alignment of the columns using a character vector of “l” (left), “c” (center), and “r” (right) (Table 5.5). Additionally, we can change the formatting. For instance, we could specify groupings for numbers that are at least 1,000 using format.args = list(big.mark = ",").

world_bank_data |>
  slice(1:10) |>
  mutate(year = as.factor(year)) |>
  kable(
    col.names = c("Country", "Year", "Inflation", "GDP growth", "Population"),
    digits = 1,
    booktabs = TRUE,
    linesep = "",
    align = c("l", "l", "c", "c", "r", "r"),
    format.args = list(big.mark = ",")
  )
Table 5.5: First ten rows of a dataset of economic indicators for Australia, Ethiopia, India, and the United States
Country Year Inflation GDP growth Population
Australia 1960 3.7 NA 10,276,477
Australia 1961 2.3 2.5 10,483,000
Australia 1962 -0.3 1.3 10,742,000
Australia 1963 0.6 6.2 10,950,000
Australia 1964 2.9 7.0 11,167,000
Australia 1965 3.4 6.0 11,388,000
Australia 1966 3.3 2.4 11,651,000
Australia 1967 3.5 6.3 11,799,000
Australia 1968 2.5 5.1 12,009,000
Australia 1969 3.3 7.0 12,263,000

5.3.3 Communicating summary statistics

After installing and loading modelsummary we can use datasummary_skim() to create tables of summary statistics from our dataset.

We can use this to get a table such as Table 5.6. That might be useful for exploratory data analysis, which we cover in Chapter 11. (Here we remove population to save space and do not include a histogram of each variable.)

world_bank_data |>
  select(-population) |> 
  datasummary_skim(histogram = FALSE)
Table 5.6:

Summary of economic indicator variables for four countries
Unique (#) Missing (%) Mean SD Min Median Max
year 62 0 1990.5 17.9 1960.0 1990.5 2021.0
inflation 243 2 6.1 6.5 -9.8 4.3 44.4
gdp_growth 224 10 4.2 3.7 -11.1 3.9 13.9

By default, datasummary_skim() summarizes the numeric variables, but we can ask for the categorical variables (Table 5.7). Additionally we can add cross-references in the same way as kable(), that is, include a “tbl-cap” entry and then cross-reference the name of the R chunk.

world_bank_data |>
  datasummary_skim(type = "categorical")
Table 5.7:

Summary of categorical economic indicator variables for four countries
country N %
Australia 62 25.0
Ethiopia 62 25.0
India 62 25.0
United States 62 25.0

We can create a table that shows the correlation between variables using datasummary_correlation() (Table 5.8).

world_bank_data |>
  datasummary_correlation()
Table 5.8:

Correlation between the economic indicator variables for four countries (Australia, Ethiopia, India, and the United States)
year inflation gdp_growth population
year 1 . . .
inflation .03 1 . .
gdp_growth .11 .01 1 .
population .25 .06 .16 1

We typically need a table of descriptive statistics that we could add to our paper (Table 5.9). This contrasts with Table 5.7 which would likely not be included in the main section of a paper, and is more to help us understand the data. We can add a note about the source of the data using notes.

datasummary_balance(
  formula = ~country,
  data = world_bank_data |> 
    filter(country %in% c("Australia", "Ethiopia")),
  dinm = FALSE,
  notes = "Data source: World Bank."
)
Table 5.9:

Descriptive statistics for the inflation and GDP dataset
Australia (N=62) Ethiopia (N=62)
Mean Std. Dev. Mean Std. Dev.
year 1990.5 18.0 1990.5 18.0
inflation 4.7 3.8 9.1 10.6
gdp_growth 3.4 1.8 5.9 6.4
population 17351313.1 4407899.0 57185292.0 29328845.8
Data source: World Bank.

5.3.4 Display regression results

We can report regression results using modelsummary() from modelsummary. For instance, we could display the estimates from a few different models (Table 5.10).

first_model <- lm(
  formula = gdp_growth ~ inflation,
  data = world_bank_data
)

second_model <- lm(
  formula = gdp_growth ~ inflation + country,
  data = world_bank_data
)

third_model <- lm(
  formula = gdp_growth ~ inflation + country + population,
  data = world_bank_data
)

modelsummary(list(first_model, second_model, third_model))
Table 5.10:

Explaining GDP as a function of inflation
(1) (2) (3)
(Intercept) 4.147 3.676 3.611
(0.343) (0.484) (0.482)
inflation 0.006 -0.068 -0.065
(0.039) (0.040) (0.039)
countryEthiopia 2.896 2.716
(0.740) (0.740)
countryIndia 1.916 -0.730
(0.642) (1.465)
countryUnited States -0.436 -1.145
(0.633) (0.722)
population 0.000
(0.000)
Num.Obs. 223 223 223
R2 0.000 0.111 0.127
R2 Adj. -0.004 0.095 0.107
AIC 1217.7 1197.5 1195.4
BIC 1227.9 1217.9 1219.3
Log.Lik. -605.861 -592.752 -590.704
F 0.024 6.806
RMSE 3.66 3.45 3.42

The number of significant digits can be adjusted with “fmt” (Table 5.11). To help establish credibility you should generally not add as many significant digits as possible (Howes 2022). Instead, you should think carefully about the data-generating process and adjust based on that.

modelsummary(
  list(first_model, second_model, third_model),
  fmt = 1
)
Table 5.11:

Three models of GDP as a function of inflation
(1) (2) (3)
(Intercept) 4.1 3.7 3.6
(0.3) (0.5) (0.5)
inflation 0.0 -0.1 -0.1
(0.0) (0.0) (0.0)
countryEthiopia 2.9 2.7
(0.7) (0.7)
countryIndia 1.9 -0.7
(0.6) (1.5)
countryUnited States -0.4 -1.1
(0.6) (0.7)
population 0.0
(0.0)
Num.Obs. 223 223 223
R2 0.000 0.111 0.127
R2 Adj. -0.004 0.095 0.107
AIC 1217.7 1197.5 1195.4
BIC 1227.9 1217.9 1219.3
Log.Lik. -605.861 -592.752 -590.704
F 0.024 6.806
RMSE 3.66 3.45 3.42

5.4 Maps

In many ways maps can be thought of as another type of graph, where the x-axis is latitude, the y-axis is longitude, and there is some outline or background image. It is possible that they are the oldest and best understood type of chart (Karsten 1923, 1). We can generate a map in a straight-forward manner. That said, it is not to be taken lightly; things quickly get complicated!

The first step is to get some data. There is some geographic data built into ggplot2 that we can access with map_data(). There are additional variables in the world.cities dataset from maps.

france <- map_data(map = "france")

head(france)
      long      lat group order region subregion
1 2.557093 51.09752     1     1   Nord      <NA>
2 2.579995 51.00298     1     2   Nord      <NA>
3 2.609101 50.98545     1     3   Nord      <NA>
4 2.630782 50.95073     1     4   Nord      <NA>
5 2.625894 50.94116     1     5   Nord      <NA>
6 2.597699 50.91967     1     6   Nord      <NA>
french_cities <-
  world.cities |>
  filter(country.etc == "France")

head(french_cities)
             name country.etc    pop   lat long capital
1       Abbeville      France  26656 50.12 1.83       0
2         Acheres      France  23219 48.97 2.06       0
3            Agde      France  23477 43.33 3.46       0
4            Agen      France  34742 44.20 0.62       0
5 Aire-sur-la-Lys      France  10470 50.64 2.39       0
6 Aix-en-Provence      France 148622 43.53 5.44       0

Using that information you can create a map of France that shows the larger cities (Figure 5.22). Use geom_polygon() from ggplot2 to draw shapes by connecting points within groups. And coord_map() adjusts for the fact that we are making a 2D map to represent a world that is 3D.

ggplot() +
  geom_polygon(
    data = france,
    aes(x = long, y = lat, group = group),
    fill = "white",
    colour = "grey"
  ) +
  coord_map() +
  geom_point(
    aes(x = french_cities$long, y = french_cities$lat),
    alpha = 0.3,
    color = "black"
  ) +
  theme_minimal() +
  labs(x = "Longitude", y = "Latitude")

Figure 5.22: Map of France showing the largest cities

As is often the case with R, there are many ways to get started creating static maps. We have seen how they can be built using only ggplot2, but ggmap brings additional functionality.

There are two essential components to a map:

  1. a border or background image (sometimes called a tile); and
  2. something of interest within that border, or on top of that tile.

In ggmap, we use an open-source option for our tile, Stamen Maps. And we use plot points based on latitude and longitude.

5.4.1 Australian polling places

In Australia, people have to go to “booths” in order to vote. Because the booths have coordinates (latitude and longitude), we can plot them. One reason we may like to do that is to notice spatial voting patterns.

To get started we need to get a tile. We are going to use ggmap to get a tile from Stamen Maps, which builds on OpenStreetMap. The main argument to this function is to specify a bounding box. A bounding box is the coordinates of the edges that you are interested in. This requires two latitudes and two longitudes.

It can be useful to use Google Maps, or other mapping platform, to find the coordinate values that you need. In this case we have provided it with coordinates such that it will be centered around Australia’s capital Canberra.

bbox <- c(left = 148.95, bottom = -35.5, right = 149.3, top = -35.1)

Once you have defined the bounding box, the function get_stamenmap() will get the tiles in that area (Figure 5.23). The number of tiles that it needs depends on the zoom, and the type of tiles that it gets depends on the type of map. We have used “toner-lite”, which is black and white, but there are others including: “terrain”, “toner”, and “toner-lines”. We pass the tiles to ggmap() which will plot it. An internet connection is needed for this to work as get_stamenmap() downloads the tiles.

canberra_stamen_map <- get_stamenmap(bbox, zoom = 11, maptype = "toner-lite")

ggmap(canberra_stamen_map)

Figure 5.23: Map of Canberra, Australia

Once we have a map then we can use ggmap() to plot it. Now we want to get some data that we plot on top of our tiles. We will plot the location of the polling place based on its “division”. This is available from the Australian Electoral Commission (AEC).

booths <-
  read_csv(
    "https://results.aec.gov.au/24310/Website/Downloads/GeneralPollingPlacesDownload-24310.csv",
    skip = 1,
    guess_max = 10000
  )

This dataset is for the whole of Australia, but as we are only plotting the area around Canberra, we will filter the data to only booths with a geography close to Canberra.

booths_reduced <-
  booths |>
  filter(State == "ACT") |>
  select(PollingPlaceID, DivisionNm, Latitude, Longitude) |>
  filter(!is.na(Longitude)) |> # Remove rows without geography
  filter(Longitude < 165) # Remove Norfolk Island

Now we can use ggmap in the same way as before to plot our underlying tiles, and then build on that using geom_point() to add our points of interest.

ggmap(canberra_stamen_map, extent = "normal", maprange = FALSE) +
  geom_point(data = booths_reduced,
             aes(x = Longitude, y = Latitude, colour = DivisionNm),
             alpha = 0.7) +
  scale_color_brewer(name = "2019 Division", palette = "Set1") +
  coord_map(
    projection = "mercator",
    xlim = c(attr(map, "bb")$ll.lon, attr(map, "bb")$ur.lon),
    ylim = c(attr(map, "bb")$ll.lat, attr(map, "bb")$ur.lat)
  ) +
  labs(x = "Longitude",
       y = "Latitude") +
  theme_minimal() +
  theme(panel.grid.major = element_blank(),
        panel.grid.minor = element_blank())

Figure 5.24: Map of Canberra, Australia, with polling places

We may like to save the map so that we do not have to create it every time, and we can do that in the same way as any other graph, using ggsave().

ggsave("map.pdf", width = 20, height = 10, units = "cm")

Finally, the reason that we used Stamen Maps and OpenStreetMap is because they are open source, but we could have also used Google Maps. This requires you to first register a credit card with Google, and specify a key, but with low usage the service should be free. Using Google Maps—by using get_googlemap() within ggmap—brings some advantages over get_stamenmap(). For instance it will attempt to find a place name rather than needing to specify a bounding box.

5.4.2 United States military bases

To see another example of a static map we will plot some United States military bases after installing and loading troopdata. We can access data about United States overseas military bases back to the start of the Cold War using get_basedata().

bases <- get_basedata()

head(bases)
# A tibble: 6 × 9
  countryname ccode iso3c basename            lat   lon  base lilypad fundedsite
  <chr>       <dbl> <chr> <chr>             <dbl> <dbl> <dbl>   <dbl>      <dbl>
1 Afghanistan   700 AFG   Bagram AB          34.9  69.3     1       0          0
2 Afghanistan   700 AFG   Kandahar Airfield  31.5  65.8     1       0          0
3 Afghanistan   700 AFG   Mazar-e-Sharif     36.7  67.2     1       0          0
4 Afghanistan   700 AFG   Gardez             33.6  69.2     1       0          0
5 Afghanistan   700 AFG   Kabul              34.5  69.2     1       0          0
6 Afghanistan   700 AFG   Herat              34.3  62.2     1       0          0

We will look at the locations of United States military bases in Germany, Japan, and Australia. The troopdata dataset already has the latitude and longitude of each base, and we will use that as our item of interest. The first step is to define a bounding box for each country.

# Use: https://data.humdata.org/dataset/bounding-boxes-for-countries
bbox_germany <- c(left = 5.867, bottom = 45.967, right = 15.033, top = 55.133)

bbox_japan <- c(left = 127, bottom = 30, right = 146, top = 45)

bbox_australia <- c(left = 112.467, bottom = -45, right = 155, top = -9.133)

Then we need to get the tiles using get_stamenmap() from ggmap.

german_stamen_map <-get_stamenmap(bbox_germany, zoom = 6, maptype = "toner-lite")

japan_stamen_map <- get_stamenmap(bbox_japan, zoom = 6, maptype = "toner-lite")

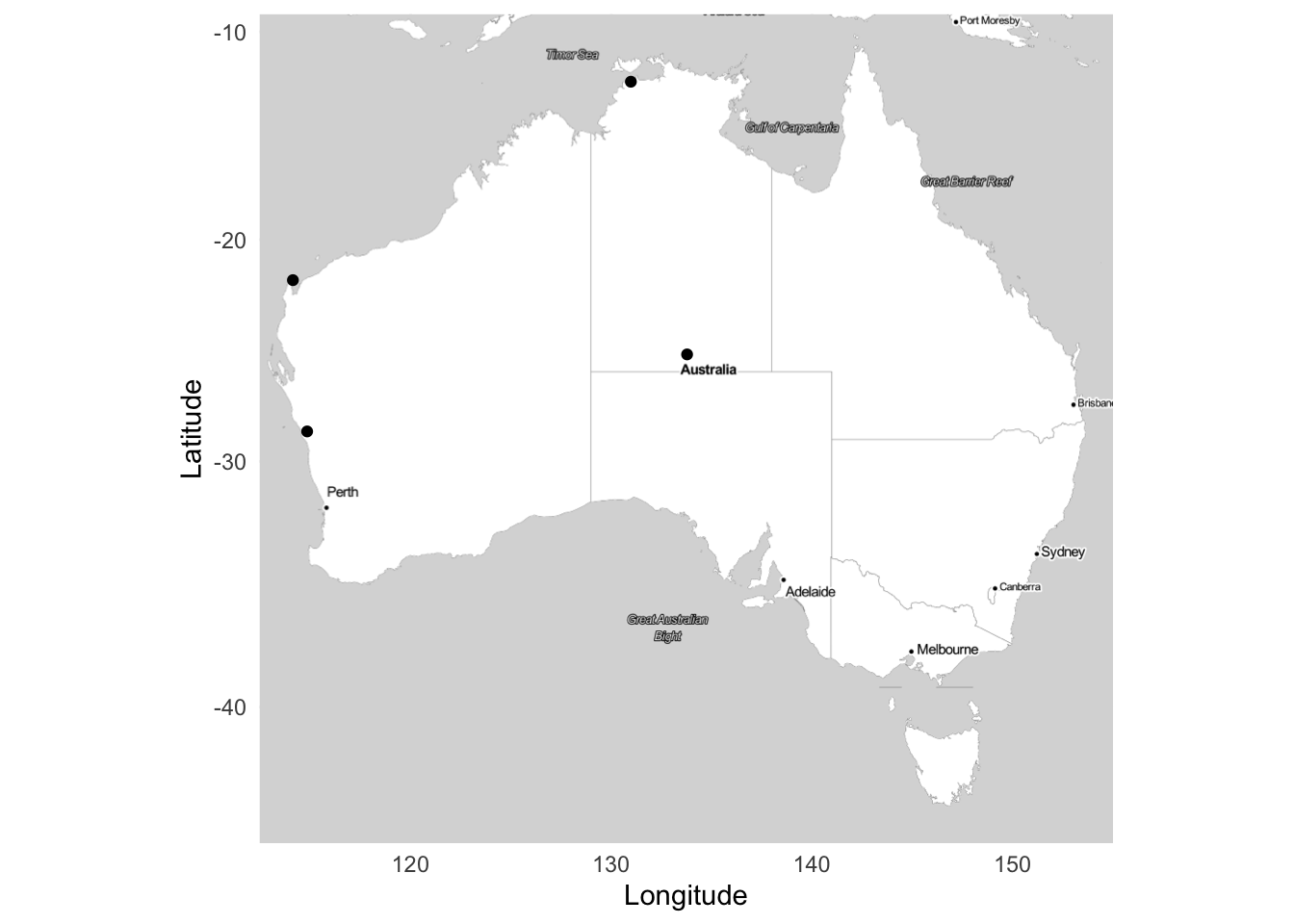
aus_stamen_map <- get_stamenmap(bbox_australia, zoom = 5, maptype = "toner-lite")

And finally, we can bring it all together with maps showing United States military bases in Germany (Figure 5.25 (a)), Japan (Figure 5.25 (b)), and Australia (Figure 5.25 (c)).

ggmap(german_stamen_map) +
  geom_point(data = bases, aes(x = lon, y = lat)) +
  labs(x = "Longitude",
       y = "Latitude") +
  theme_minimal()

ggmap(japan_stamen_map) +
  geom_point(data = bases, aes(x = lon, y = lat)) +
  labs(x = "Longitude",
       y = "Latitude") +
  theme_minimal()

ggmap(aus_stamen_map) +
  geom_point(data = bases, aes(x = lon, y = lat)) +
  labs(x = "Longitude",
       y = "Latitude") +
  theme_minimal()

(a) Germany

(b) Japan

(c) Australia

Figure 5.25: Map of United States military bases in various parts of the world

5.4.3 Geocoding

So far we have assumed that we already have geocoded data. This means that we have latitude and longitude coordinates for each place. But sometimes we only have place names, such as “Sydney, Australia”, “Toronto, Canada”, “Accra, Ghana”, and “Guayaquil, Ecuador”. Before we can plot them, we need to get the latitude and longitude coordinates for each case. The process of going from names to coordinates is called geocoding.

Oh, you think we have good data on that!

While you almost surely know where you live, it can be surprisingly difficult to specifically define the boundaries of many places. And this is made especially difficult when different levels of government have different definitions. Bronner (2021) illustrates this in the case of Atlanta, Georgia, where there are (at least) three official different definitions:

  1. the metropolitan statistical area;
  2. the urbanized area; and
  3. the census place.

Which definition is used can have a substantial effect on the analysis, or even the data that are available, even though they are all “Atlanta”.

There are a range of options to geocode data in R, but tidygeocoder is especially useful. We first need a dataframe of locations.

place_names <-
  tibble(
    city = c("Sydney", "Toronto", "Accra", "Guayaquil"),
    country = c("Australia", "Canada", "Ghana", "Ecuador")
  )

place_names
# A tibble: 4 × 2
  city      country  
  <chr>     <chr>    
1 Sydney    Australia
2 Toronto   Canada   
3 Accra     Ghana    
4 Guayaquil Ecuador  
place_names <-
  geo(
    city = place_names$city,
    country = place_names$country,
    method = "osm"
  )

place_names
# A tibble: 4 × 4
  city      country      lat    long
  <chr>     <chr>      <dbl>   <dbl>
1 Sydney    Australia -33.9  151.   
2 Toronto   Canada     43.7  -79.4  
3 Accra     Ghana       5.56  -0.201
4 Guayaquil Ecuador    -2.19 -79.9

And we can now plot and label these cities (Figure 5.26).

world <- map_data(map = "world")

ggplot() +
  geom_polygon(
    data = world,
    aes(x = long, y = lat, group = group),
    fill = "white",
    colour = "grey"
  ) +
  geom_point(
    aes(x = place_names$long, y = place_names$lat),
    color = "black") +
  geom_text(
    aes(x = place_names$long, y = place_names$lat, label = place_names$city),
    nudge_y = -5) +
  theme_minimal() +
  labs(x = "Longitude",
       y = "Latitude")

Figure 5.26: Map of Accra, Sydney, Toronto, and Guayaquil after geocoding to obtain their locations

5.5 Concluding remarks

In this chapter we have covered a lot of ground, focused on communicating data. We spent a lot of time on graphs, because of their ability to convey a large amount of information in an efficient way. We then turned to tables because of how they can specifically convey information. Finally, we discussed maps, which allow us to display geographic information. The most important task is to show the observations to the full extent possible.

5.6 Exercises

Scales

  1. (Plan) Consider the following scenario: Three friends—Edward, Hugo, and Lucy—each measure the height of 20 of their friends. Each of the three use a slightly different approach to measurement and so make slightly different errors. Please sketch what that dataset could look like and then sketch a graph that you could build to show all observations.
  2. (Simulate) Please further consider the scenario described and simulate the situation with every variable independent of each other. Please include three tests based on the simulated data.
  3. (Acquire) Please describe a possible source of such a dataset.
  4. (Explore) Please use ggplot2 to build the graph that you sketched using the data that you simulated.
  5. (Communicate) Please write two paragraphs about what you did.

Questions

  1. Assume the tidyverse and datasauRus are installed and loaded. What would be the outcome of the following code datasaurus_dozen |> filter(dataset == "v_lines") |> ggplot(aes(x=x, y=y)) + geom_point()?
    1. Four vertical lines
    2. Five vertical lines
    3. Three vertical lines
    4. Two vertical lines
  2. Which theme does not have solid lines along the x and y axes (pick one)?
    1. theme_minimal()
    2. theme_classic()
    3. theme_bw()
  3. Assume the tidyverse and the beps dataset as generated in this chapter have been installed and loaded. Which argument should be added to geom_bar() in the following code to make the bars for the different parties be next to each other rather than on top of each other beps |> ggplot(mapping = aes(x = age, fill = vote)) + geom_bar()?
    1. position = "side_by_side"
    2. position = "dodge2"
    3. position = "adjacent"
    4. position = "closest"
  4. In the code below, what should be added to labs() to change the text of the legend?
    1. color = "Voted for"
    2. legend = "Voted for"
    3. scale = "Voted for"
    4. fill = "Voted for"
beps |>
  ggplot(mapping = aes(x = age, fill = vote)) +
  geom_bar() +
  theme_minimal() +
  labs(x = "Age of respondent", y = "Number of respondents")
  1. Based on the help file for scale_colour_brewer() which palette diverges?
    1. “Accent”
    2. “RdBu”
    3. “GnBu”
    4. “Set1”
  2. Which geom should be used to make a scatter plot?
    1. geom_smooth()
    2. geom_point()
    3. geom_bar()
    4. geom_dotplot()
  3. Which of these would result in the largest number of bins?
    1. geom_histogram(binwidth = 5)
    2. geom_histogram(binwidth = 2)
  4. Suppose there is a dataset that contains the heights of 100 birds, each from one of three different species. If we are interested in understanding the distribution of these heights, then in a paragraph or two, please explain which type of graph should be used and why.
  5. Would this code data |> ggplot(aes(x = col_one)) |> geom_point() if we assume the dataset and columns exist (pick one)?
    1. Yes
    2. No
  6. Which of the following, if any, are elements of the layered grammar of graphics of Wickham (2010) (select all that apply)?
    1. A default dataset and set of mappings from variables to aesthetics.
    2. One or more layers, with each layer having one geometric object, one statistical transformation, one position adjustment, and optionally, one dataset and set of aesthetic mappings.
    3. Colors that enable the reader to understand the main point.
    4. A coordinate system.
    5. The facet specification.
    6. One scale for each aesthetic mapping used.
  7. Which function from modelsummary could we use to create a table of descriptive statistics?
    1. datasummary_descriptive()
    2. datasummary_skim()
    3. datasummary_crosstab()
    4. datasummary_balance()

Tutorial

Please create a graph using ggplot2 and a map using ggmap and add explanatory text to accompany both. Be sure to include cross-references and captions, etc. Each of these should take about pages.

Then, with regard the graph you created, please reflect on Vanderplas, Cook, and Hofmann (2020). Add a few paragraphs about the different options that you considered to make the graph more effective.

And finally, with regard to the map that you created, please reflect on the following quote from Heather Krause, founder of We All Count: “maps only show people who aren’t invisible to the makers” as well as Chapter 3 from D’Ignazio and Klein (2020) and add a few paragraphs related to this.

Use Quarto, and include an appropriate title, author, date, and citations. Submit a PDF.

Paper

At about this point the Mawson Paper from Online Appendix D would be appropriate.